ஆதி (கணிதம்)
கணிதத்தில் யூக்ளிடிய வெளியின் ஆதி அல்லது ஆதிப்புள்ளி (origin) என்பது ஒரு சிறப்புப் புள்ளி. இடவெளியில் அமையும் அனைத்துப் புள்ளிகளின் அமைவும் இப்புள்ளியை ஆதாரமாகக் கொண்டு தீர்மானிக்கப்படுகிறது. இப்புள்ளியின் வழக்கமான குறியீடு O. கார்ட்டீசியன் ஆள்கூற்று முறைமையில் அதன் அச்சுகள் வெட்டிக்கொள்ளும் புள்ளியாக இது அமையும். யூக்ளிடிய வெளியில் எந்தவொரு புள்ளியும் ஆதிப்புள்ளியாகக் கட்டற்றுத் தேர்ந்தெடுக்கப் படலாம்.

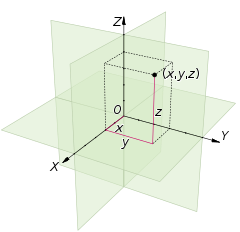
பெரும்பாலும் வழக்கமான ஆயமுறைமைகள் இருபரிமாணம் அல்லது முப்பரிமாணத்தில் உள்ளன. இருபரிமாண ஆயமுறைமை ஒரு தளத்தில் அமைந்த இரு செங்குத்து அச்சுகளையும் முப்பரிமாண ஆயமுறைமை ஒரு இடவெளியில் அமைந்த மூன்று செங்குத்து அச்சுகளையும் கொண்டிருக்கும். ஆதிப்புள்ளி இந்த அச்சுகள் ஒவ்வொன்றையும் நேர் அரைஅச்சு மற்றும் எதிர் அரைஅச்சு என இரண்டு சமபகுதிகளாகப் பிரிக்கும். ஆதிப் புள்ளியை ஆதாரமாகக் கொண்டு மற்ற புள்ளிகளின் இருப்பிடத்தை அவற்றின் அச்சுதூரங்கள் மூலம் குறிக்கலாம். ஒரு புள்ளியின் ஒவ்வொரு அச்சின் மீதான வீழல்கள் (நேர் அரைஅச்சு அல்லது எதிர் அரைஅச்சின் மீதானவை) அப்புள்ளிக்குரிய அந்தந்த அச்சுதூரங்கள் எனப்படும். ஆதிப்புள்ளியின் அச்சுதூரங்கள் எப்பொழுதும் பூச்சியமாகவே இருக்கும். ஆதிப்புள்ளியின் அச்சுதூரங்கள் இரு பரிமாணத்தில் (0,0) மற்றும் முப்பரிமாணத்தில் (0,0,0).[1][2][3]
கலெப்பெண் தளத்தில் மெய் அச்சும் கற்பனை அச்சும் வெட்டிக்கொள்ளும் புள்ளி ஆதிப்புள்ளி. இப்புள்ளி 0 + 0i என்ற கலப்பெண்ணால் குறிக்கப்படுகிறது..
ஆதிப்புள்ளியைப் பொறுத்த சமச்சீர்
தொகுஆதிப்புள்ளியைப் பொறுத்து சமச்சீரான ஒரு வரைபடத்தை 180 பாகைகள் சுழற்றினால் அதன் தோற்றத்தில் எந்தவொரு மாற்றமும் இருக்காது. ஒரு வரைபடம் x-அச்சு மற்றும் y -அச்சு இரண்டிலும் பிரதிபலிக்கப்படும்போது அதன் தோற்றத்தில் எந்தவொரு மாற்றமும் இல்லையெனில் அந்த வரைபடம் ஆதிப்புள்ளியைப் பொறுத்து சமச்சீரானது.
நேர்மாறு சார்புடைய சார்புகளும் அவற்றின் நேர்மாறுகளும் கோடு y = x கோட்டைப் பொறுத்து சமச்சீரானவையாக இருக்கும். இக்கோடு ஆதிப்புள்ளி வழியே செல்லும் கோடாகும்.
மேற்கோள்கள்
தொகு- ↑ Madsen, David A. (2001), Engineering Drawing and Design, Delmar drafting series, Thompson Learning, p. 120, பன்னாட்டுத் தரப்புத்தக எண் 9780766816343.
- ↑ Pontrjagin, Lev S. (1984), Learning higher mathematics, Springer series in Soviet mathematics, Springer-Verlag, p. 73, பன்னாட்டுத் தரப்புத்தக எண் 9783540123514.
- ↑ Tanton, James Stuart (2005), Encyclopedia of Mathematics, Infobase Publishing, பன்னாட்டுத் தரப்புத்தக எண் 9780816051243.