கோஷியின் இடைமதிப்புத் தேற்றம்

வகை நுண்கணிததில் கோஷியின் இடைமதிப்புத் தேற்றம் (Cauchy's mean value theorem) அல்லது நீட்டிக்கப்பட்ட இடைமதிப்புத் தேற்றம் (extended mean value theorem) என்பது இடைமதிப்புத் தேற்றத்தின் பொதுமைப்படுத்தலாகும்.

கோஷியின் இடைமதிப்புத் தேற்றத்தின் வடிவவியல் விளக்கம்

இத்தேற்றத்தின் கூற்று:

$f,\,$ $g\,$ சார்புகள்,

• மூடிய இடைவெளி [a,b] -ல் தொடர்ச்சியானவையாகவும்;
• திறந்த இடைவெளி (a, b) ல் வகையிடத்தக்கவையாகவும் இருந்தால்,

$(f(b)-f(a))g\,'(c)=(g(b)-g(a))f\,'(c).\,$

என்றவாறு ஒரு மதிப்பு, c ∈ (a,b) காணமுடியும்.

$\displaystyle g(a)\neq g(b)$ மற்றும் $\displaystyle g'(x_{0})\neq 0$ எனில் இம்முடிவை,

${\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}\cdot$ என மாற்றி எழுதலாம்.

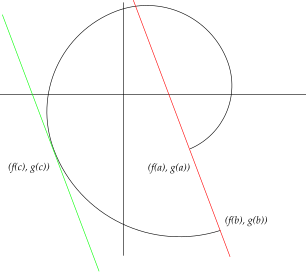
வடிவவியல் முறையில் இது, (f(a),g(a)), (f(b),g(b)) புள்ளிகளை இணைக்கும் கோட்டிற்கு இணையாக

${\begin{array}{ccc}[a,b]&\longrightarrow &\mathbb {R} ^{2}\\t&\mapsto &{\bigl (}f(t),g(t){\bigr )},\end{array}}$ என்ற வளைவரைக்கு ஏதாவது ஒரு தொடுகோடு இருக்கும் என்பதைக் காட்டுகிறது.

எனினும், வெவ்வேறானவையாக இருக்கும் அனைத்து (f(a),g(a)) and (f(b),g(b)) -க்கும் இதுபோன்ற இணைத்தொடுகோடு அமையும் என கோஷியின் தேற்றம் கூறவில்லை. ஏனென்றால் $\ f^{\prime }(x)=g^{\prime }(x)=0$ என அமையும் c மதிப்புகளுக்கு மட்டும்தான் அதாவது மேலே தரப்பட்ட வளைவரையின் நிலைப் புள்ளிகளில்தான் அவ்வாறு இருக்க முடியும். அந்த மாதிரியான புள்ளிகளில் தொடுகோடுகள் இல்லாமலே இருக்கலாம்

எடுத்துக்காட்டு வளைவரை:

$t\mapsto (t^{3},1-t^{2}),$ என்ற வளைவரை, [−1,1] இடைவெளியில் (−1,0) லிருந்து (1,0) க்குச் செல்கிறது. இவ்வளைவரைக்கு நிலைப் புள்ளி உள்ளது. மேலும் t = 0-ல் ஒரு கூர் உள்ளது. இருப்பினும் அதற்கு கிடைமட்டத் தொடுகோடு இல்லை.

கோஷியின் தேற்றத்தைப் பயன்படுத்தி லாபிதாலின் விதியை நிறுவலாம்.g(t) = t. எனில் கோஷியின் இடைமதிப்புத் தேற்றத்தின் ஒரு சிறப்புவகை இடைமதிப்புத் தேற்றமாகும்.

நிறுவல்

$\ h(x)=f(x)-rg(x),$ r ஒரு மாறிலி, எனக் கொள்க.

$f,\,$ $g\,$ சார்புகள், இடைவெளி [a, b] -ல் தொடர்ச்சியானவையாகவும்; திறந்த இடைவெளி (a, b) ல் வகையிடத்தக்கவையாகவும் இருப்பதால் $h,\,$ -ம் அதே நிபந்தனைகளுக்குக் கட்டுப்படும்.

$\ h(a)=h(b)$ என்றவாறு r -ன் மதிப்பை எடுத்துக்கொள்ள வேண்டும்.

${\begin{aligned}h(a)=h(b)&\iff f(a)-rg(a)=f(b)-rg(b)\\&\iff r(g(b)-g(a))=f(b)-f(a)\\&\iff r={\frac {f(b)-f(a)}{g(b)-g(a)}}\cdot \end{aligned}}$

ரோலின் தேற்றத்தின் நிபந்தனைகள் மூன்றையும் $h,\,$ நிறைவு செய்வதால், ரோலின் தேற்ற முடிவின்படி:

ஏதாவது ஒரு மதிப்பு, c ∈ (a,b) -க்கு

$\ h'(c)=0$,

$\ h(x)=f(x)-rg(x)$ லிருந்து:

$h'(c)=0=f'(c)-r(g'(c))\Rightarrow {\frac {f'(c)}{g'(c)}}=r={\frac {f(b)-f(a)}{g(b)-g(a)}}$

என தேற்றம் நிறுவப்படுகிறது.

வெளி இணைப்புகள்

• PlanetMath: Mean-Value Theorem பரணிடப்பட்டது 2009-11-18 at the வந்தவழி இயந்திரம்
• Weisstein, Eric W., "Mean value theorem", MathWorld.
• Weisstein, Eric W., "Cauchy's Mean-Value Theorem", MathWorld.
• "Mean Value Theorem: Intuition behind the Mean Value Theorem" at the Khan Academy