துணிப்புத் தகைவு

துணிப்புத் தகைவு (shear stress) அல்லது நறுக்குத் தகைவு அல்லது வெட்டுத் தகைவு என்பது ஒரு பொருளின் பரப்பளவிற்கு செங்குத்தாகவும் வெட்டுமுகத்துக்கு இணையாகவும் செயல்படும் தகைவு ஆகும்.

துணிப்புத் தகைவு
பொதுவான குறியீடு:	τ
SI அலகு:	பாசுகல்
வேறு அலகுகளிலிருந்து பெறப்படும் வாய்ப்பாடு:	τ = F/A

இணைத்தகைவால் சேதம் அடைந்துள்ள சாலை

அடிப்பக்கம் நிலையாக பொருத்தப்பட்ட ஒரு செவ்வகத்துக்கு மேற்பகுதியில் துணிப்பு விசை தரப்பட்டுள்ளது. இதனால் விளையும் துணிப்புத் தகைவு, τ, செவ்வகத்தை உருமாற்றி இணைகரம் ஆக்குகிறது. இது செவ்வக மேற்பகுதிப் பரப்பில் செயல்படுகிறது.

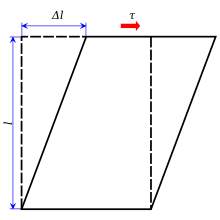
துணிப்புத் தகைவு துணிப்பு விசைகளால் ஏற்படுகிறது. இந்த விசைகள் பொருளின் வெட்டுமுகத்துக்கு இணையாக எதிரெதிராகச் செயல்படும் சம அளவு விசைகளாகும்.

கத்திரிக்கோல் துணிப்புத் தகைவு தாளுக்குச் செங்குத்தாகவும் தாள் வெட்டுமுகத்திக்கு இணையாகவும் செயல்படுகிறது.

நீர்மம் ஒன்று ஒரு பரப்பில் நகரும் போது, எதிர்ப்படும் பொருட்பரப்புக்குச் செங்குத்தாகச் செயல்பட்டு அது துணிப்புத் தகைவை உண்டாக்குகிறது. மழைநீரால் ஏற்படும் நில அரிப்பு, சாலைத் துண்டிப்பு ஆகியவை இவ்வாறே உண்டாகின்றன.

பொதுத் துணிப்புத் தகைவு

நிரல் (சராசரி) துணிப்புத் தகைவு அல்குப் பரப்பில் செயல்படும் விசையாகும்.:

$\tau ={F \over A},$

இங்கு,

τ = துணிப்புத் தகைவு;

F = தரப்பட்ட விசை;

A = அந்த விசை நெறியனுக்கு இணையாக அமையும் பொருளின் குறுக்கு வெட்டுமுகத்தின் பரப்பாகும்.

பிற வடிவங்கள்

தூய நிலை

தூயத் துணிப்புத் தகைவு, தூயத் துணிப்புத் திரிபுக்குக் ( γ ) கீழுள்ள சமன்பாட்டால் உறவுபடுத்தப்படுகிறது:

$\tau =\gamma G\,$

இங்கு, G என்பது ஒருபடித்தான பொருளின் துணிப்பு மட்டு ஆகும். துணிப்பு மட்டு கீழுள்ள வாய்பாட்டால் தரப்படுகிறது.

$G={\frac {E}{2(1+\nu )}}.$

இங்கு, E என்பது யங் மட்டு ஆகும்; ν என்பது பாயிசான் விகிதம் ஆகும்.

விட்டத்தின் துணிப்புத் தகைவு

விட்டத் துணிப்புத் தகைவு என்பது விட்டத்துக்குத் தந்த துணிப்பு விசை உருவாக்கும் அகத் துணிப்புத் தகைவாக வரையறுக்கப்படுகிறது.

$\tau ={fQ \over Ib},$

இங்கு,

f = குறிபிட்ட இடத்தில் செயல்படும் மொத்தத் துணிப்பு விசையாகும்;

Q = பரப்பின் நிலையியல் திருப்புமை (திருப்புதிறன்) ஆகும்;

b = துணிப்புக்குச் செங்குத்தாக அமையும் பொருளின் தடிப்பு (அகலம்) ஆகும்;

I =மொத்த வெட்டுமுகப் பரப்பின் உறழ்வுத் திருப்புமை ஆகும்.

விட்டத் துணிப்புத் தகைவின் வாய்பாடு சுராவ்சுகி துணிப்புத் தகைவு வாய்பாடு எனப்படுகிறது. இந்த வாய்பாட்டை 1855 இல் திமித்ரி இவனோவிச் சுராவ்சுகி முதன்முதலாக கணித வாய்பாடாகக் கொணர்ந்தார்.

பகுதி மேலோட்டுத் துணிப்புத் தகைவு

பகுதி மேலோட்டுக் கட்டமைப்பின் துணிப்புத் தகைவுகளைக் கருத்தியலாக கட்டமைப்பின் வெட்டுமுகத்தை அச்சுச் சுமை தாங்கும் சரங்களாகவும் துணிப்புப் பாய்வு ஏந்தும் சட்டங்களாகவும் கருதிக் கணக்கிடலாம். துணிப்புப் பாய்வை மேலோட்டுக் கட்டமைப்பின் தடிப்பால் வகுக்க துணிப்புத் தகைவின் மதிப்பைப் பெறலாம். எனவே பெருமத் துணிப்புத் தகைவு சட்ட்த்தில் பெஉமத் துணிப்புப் பாய்வு உள்ள இடத்திலோ அல்லது சிறுமத் தடிப்பு உள்ள இடத்திலோ அமையும்.

மண்தரையில் அமையும் கட்டுமானங்களும் துணிப்புத் தகைவால் இற்றுப் போகலாம்; மண்நிரப்பிய அணையின் எடை அடிமண் குலைவை, சிறுநிலச்சரிவைப் போல, உருவாக்கலாம்.

மொத்தல் துணிப்புத் தகைவு

மொத்தலுக்கு ஆட்பட்ட திண்ம வட்டத் தண்டின் பெருமத் துணிப்புத் தகைவு சமைன்பாடு:

$\tau ={\sqrt {2UG \over V}},$

இங்கு,

U =இயக்க ஆற்றல் மாற்றம்;

G =துணிப்பு மட்டு;

V = தண்டின் பருமனளவு;

மேலும்,

U = U_{சுழல்வு} + U_{தந்தது};

U_{சுழல்வு} = 1/2Iω²;

U_{தந்தது} = Tθ_{பெயர்ந்தது};

I = பொருண்மை உறழ்வுத் திருப்புமை;

ω = கோண வேகம்.

பாய்மங்களில் துணிப்புத் தகைவு

எடுத்துகாட்டு

கார்த்தேய ஆயங்களில்(x,y) ஓர் இருபருமான வெளியைக் கருதுவோம்.இதில் அமையும் பாய்வு விரைவு உறுப்புகள் (u,v)) ஆகும்; இதன் துணிப்புத் தகைவு பின்வரும் எண்சாரத்தால் தரப்படும்:

${\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x{\frac {\partial u}{\partial x}}&0\\0&-t{\frac {\partial v}{\partial y}}\end{pmatrix}}$

இந்தச் சமன்பாடு நியூட்டனியல் பாய்வைக் குறிக்கிறது. நடப்பில் இதைப் பின்வருமாறும் கோவைப்படுத்தலாம்:

${\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}\cdot {\begin{pmatrix}{\frac {\partial u}{\partial x}}&{\frac {\partial u}{\partial y}}\\{\frac {\partial v}{\partial x}}&{\frac {\partial v}{\partial y}}\end{pmatrix}}$,

இது ஒருபடித்தல்லாத பாய்வுக்கான பிசுப்புக்கான உயர்நெறிய (tensor)னாகும்:

${\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}$

இது சீரிலாத பெயர்நிலைப் (transient) பாய்வைக் குறிக்கிறது; இது உண்மையில் பாய்வு, அதன் விரைவுகளைச் சாராதிருத்தலைக் காணலாம்:

$\mathbf {\mu } (x,t)={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}$

இது நியூட்டனியப் பாய்வாகும். இதன் பிசுப்புமை பின்வருமாறு:

${\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{u}}&0\\0&{\frac {1}{u}}\end{pmatrix}}$

இதில் பிசுப்புமை, பாய்வு விரைவைச் சார்ந்துள்ளதால் நியூட்டனியல் சாராத பாய்வாகும். மேலும், இந்தப் பாய்வு ஒருபடித்தானதாகும்.இந்த எண்சாரம் முற்றொருமை எண்சாரமாக அமைவதால், இதன் பிசுப்புமை பின்வருமாறு அளவனாக அமைகிறது:

$\mu (u)={\frac {1}{u}}$.

உணரிகளால் அளத்தல்

நுண்கம்பத் துணிப்புத் தகைவு உணரி

அடுத்த நுட்பம் மென்சுவரில் நிறுவிய நெகிழ்தகவு பலபடிமப் பொருள்களால் ஆகிய நுண்கம்பங்கள் தரப்பட்ட இழுப்பு விசைகளின் கீழ் சுவரின் அருகாமையில் வளையும் திறத்தைப் பயன்படுத்துகிறது. இது சுவரருகு விரைவுச் சரிமானங்களையும் களச் சுவரின் துணிப்புத் தகைவையும் பயன்படுத்துவதால், இந்த உணரி மறைமுக அளத்தல் நெறிமுறையைச் சார்ந்ததாகும்,