வெட்டு (கணக் கோட்பாடு)

கணிதத்தில் A , B ஆகிய இரு கணங்களின் வெட்டு அல்லது வெட்டு கணம் (intersection) A ∩ B என்பது, A , B இரண்டிலுமுள்ள பொதுவான உறுப்புகள் மட்டும் கொண்ட கணமாகும்.

A , B என்ற இரு கணங்களின் வெட்டு:
$~A\cap B$

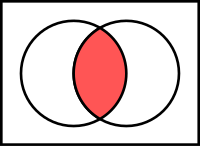
வரையறை

இரு கணங்களின் வெட்டுக்கான ஒரு எடுத்துக்காட்டு

A , B கணங்களின் வெட்டுக்கான குறியீடு: $A\cap B$

$A\cap B=\{x:x\in A\,\land \,x\in B\}$

x ∈ A மற்றும் x ∈ B என இருந்தால், இருந்தால் மட்டுமே, x ∈ A ∩ B.

அதாவது, A மற்றும் B இரண்டுக்கும் பொதுவான உறுப்பாக இருந்தால் மட்டுமே x ஆனது A ∩ B இன் உறுப்பாகும்.

எடுத்துக்காட்டு:

• A ={1, 2, 3}, B = {2, 3, 4} எனில், A ∩ B = {2, 3}.
• பகா எண்களின் கணம் {2, 3, 5, 7, 11, ...}, ஒற்றை எண்களின் கணம் {1, 3, 5, 7, 9, 11, ...} இரண்டின் வெட்டு கணத்தில் எண் 9 ஒரு உறுப்பாகாது.

மூன்று கணங்களின் வெட்டு:
$~A\cap B\cap C$

கிரேக்க,ஆங்கில, உருசிய அகரவரிசை எழுத்துக்களின் கணங்களின் வெட்டு கணம். உச்சரிப்பைத் தவிர்த்து, எழுத்துகளின் வடிவம் மட்டுமே கருத்தில் கொள்ளப்படுகிறது.

ஒரே சமயத்தில் இரண்டுக்கும் மேற்பட்ட கணங்களுக்கும் வெட்டு காணமுடியும்.

• A, B, C, என்ற மூன்று கணங்களின் வெட்டு:

A ∩ B ∩ C  = A ∩ (B ∩ C)

• A, B, C, D என்ற நான்கு கணங்களின் வெட்டு:

A ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)).

பண்புகள்

• A ∩ B   என்னும் கணம்   A  ,   B   இன் உட்கணம் ஆகும்.

$A\cap B\subseteq A,$ $A\cap B\subseteq B$

• $A\cap A=A$
• $A\cap \emptyset =\emptyset$
• கணங்களின் வெட்டு காணும் செயல் பரிமாற்றுப் பண்பு உடையது

$A\cap B=B\cap A$

• கணங்களின் வெட்டு காணும் செயல் சேர்ப்புப் பண்பு உடையது

$A\cap (B\cap C)=(A\cap B)\cap C$

• த மோர்கனின் விதிப்படி, A , B கணங்களின் வெட்டு கணமானது, அக்கணங்களின் நிரப்பு கணங்களின் ஒன்றிப்பின் நிரப்பு கணமாக இருக்கும்.

$A\cap B=(A^{c}\cup B^{c})^{c}$

மேலும் படிக்க

• Devlin, K. J. (1993). The Joy of Sets: Fundamentals of Contemporary Set Theory (Second ed.). New York, NY: Springer-Verlag. பன்னாட்டுத் தரப்புத்தக எண் 3-540-94094-4.
• Munkres, James R. (2000). "Set Theory and Logic". Topology (Second ed.). Upper Saddle River: Prentice Hall. பன்னாட்டுத் தரப்புத்தக எண் 0-13-181629-2.
• Rosen, Kenneth (2007). "Basic Structures: Sets, Functions, Sequences, and Sums". Discrete Mathematics and Its Applications (Sixth ed.). Boston: McGraw-Hill. பன்னாட்டுத் தரப்புத்தக எண் 978-0-07-322972-0.

வெளியிணைப்புகள்

• Weisstein, Eric W., "Intersection", MathWorld.