கலப்புக் கோட்டுரு

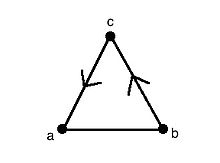
திசையற்ற மற்றும் திசையுள்ள விளிம்புகளைக் கொண்ட கோட்டுருவானது கலப்புக் கோட்டுரு (mixed graph) என அழைக்கப்படும். படத்திலுள்ள கலப்புக் கோட்டுருவின் மூன்று விளிம்புகளில் இரண்டு திசை விளிம்புகளாகவும் ஒன்று திசையற்ற விளிம்பாகவும் இருப்பதைக் காணலாம்.

வரையறை தொகு

கலப்புக் கோட்டுரு G = (V, E, A) என்ற மும்மையாகும். இதில்^[1]:

$V$ - முனைகளின் கணம்;
$E$ - திசையற்ற விளிம்புகளின் கணம்
$A$ - திசை விளிம்புகளின் கணம்

கலப்புக் கோட்டுருவில் $u,v\in V$ இரு அண்மை முனைகள் எனில்:

இவ்விரு முனைகளை இணைக்கும் திசை விளிம்பு (directed edge) அல்லது வில் (arc) என்பது திசைப்போக்குடைய விளிம்பாகும். இதன் குறியீடுகள்: ${\overrightarrow {uv}}$ அல்லது $(u,v)$ . இதில் $u$ வில்லின் வால்முனை; $v$ தலைமுனை.^[2]
இவ்விரு முனைகளை இணைக்கும் திசையற்ற விளிம்பு (undirected edge) அல்லது சுருக்கமாக விளிம்பு (edge) என்பது திசைப்போக்கற்ற விளிம்பாகும். இதன் குறியீடுகள்: $uv$ or $[u,v]$ .^[2]

கலப்புக் கோட்டுருவில் நடை என்பது $v_{0},c_{1},v_{1},c_{2},v_{2},\dots ,c_{k},v_{k}$ என்ற முனைகள் மற்றும் விளிம்புகளின் தொடர்முறையாகும். இத்தொடர்முறையில் $v_{0},,v_{1},,v_{2},\dots ,v_{k}$ கலப்புக் கோட்டுருவின் முனைகள்; மேலும் அனைத்து $i$ களுக்கும் $c_{i}=v_{i}v_{i+1}$ என்பது கலப்புக் கோட்டுருவின் விளிம்பாகவோ அல்லது $c_{i}={\overrightarrow {v_{i}v_{i+1}}}$ திசைவிளிம்பாகவோ இருக்கும். முதல் மற்றும் இறுதி முனைகள் தவிர வேறெந்த முனைகளோ, விளிம்புகளோ அல்லது விற்களோ மீண்டும் வராத பாதையானது "நடை" எனப்படுகிறது. முதல் மற்றும் இறுதி முனைகள் இரண்டும் ஒரே முனையாக அமைந்தால் அப்பாதையானது "மூடிய பாதை"யாகும். முதல் மற்றும் இறுதி முனைகளைத் தவிர வேறெந்த முனைகளும் மீண்டும் வராத மூடிய பாதையானது சுழற்சியாகும். ஒரு கலப்புக் கோட்டுருவில் சுழற்சிகளே இல்லையெனில் அது "சுழற்சியற்றக் கலப்புக் கோட்டுரு" என அழைக்கப்படும்.

நிறந்தீட்டல் தொகு

கலப்புக் கோட்டுருவிற்கு நிறந்தீட்டலை அதன் முனைகளுக்கு பெயரிடலாக அல்லது வெவ்வேறு $k$ (நேர் முழு எண்) நிறங்களை அதன் முனைகளுக்கு அளிப்பதாகவோ எடுத்துக்கொள்ளலாம்.^[3] விளிம்புகளால் இணைக்கப்படும் முனைகள் ஒவ்வொன்றுக்கும் வெவ்வேறு நிறங்கள் தரப்பட வேண்டும். அளிக்கப்படும் நிறங்கள் $1$ முதல் $k$ வரையான எண்களால் குறிக்கப்பட வேண்டும். ஒரு திசை விளிம்பில் அதன் வால்முனைக்கு அளிக்கப்படும் எண் அதன் தலைமுனைக்கு அளிக்கப்படும் எண்ணைவிட சிறியதாக இருக்குமாறு கலப்புக் கோட்டுவை நிறந்தீட்ட வேண்டும்.^[3]

எடுத்துக்காட்டு தொகு

கலப்புக் கோட்டுரு நிறந்தீட்டல்

அருகிலுள்ள படத்தில் ஒரு கலப்புக் கோட்டுருவின் முனைகளுக்கு எண்கள் தரப்பட்டு நிறந்தீட்டப்பட்டுள்ளது. இக்கோட்டுருவிற்கு நிறந்தீட்ட எடுத்துக்கொள்ளப்பட்ட எண்கள் $\{1,2,3\}$ . $u$ மற்றும் $v$ முனைகள் விளிம்பால் இணைக்கப்பட்டிருப்பதால் அவற்றுக்கு மாறுபட்ட நிறங்கள் அல்லது எண்கள் அளிக்கப்பட வேண்டும். அவற்றுக்கு முறையே 1, 2 என்ற எண்கள் அளிக்கப்பட்டுள்ளன. $v$ மற்றும் $w$ இரண்டும் ஒரு வில்லால் இணைக்கப்பட்டுள்ளன. எனவே வால் முனைக்கு ( $v$ ) சிறிய எண்ணும் தலைமுனைக்கு ( $w$ ) பெரிய எண்ணும் அளிக்கப்பட வேண்டும். $v,$ $w$ இரண்டுக்கும் முறையே 2, 3 என்ற எண்கள் அளிக்கப்பட்டுள்ளன.

நிறந்தீட்டல் இருத்தல் தொகு

ஒரு கலப்புக் கோட்டுருவை நிறந்தீட்ட முடியலாம் அல்லது முடியாமலும் இருக்கலாம். ஒரு கலப்புக் கோட்டுருவில் திசையுள்ள சுழற்சிகள் இல்லாமல் இருந்தால் மட்டுமே அக்கோட்டுருவிற்கு k-நிறந்தீட்டல் இருக்கும்.^[2] அவ்வாறு ஒரு k-நிறந்தீட்டல் இருக்கும்பட்சத்தில் அக்கலப்புக் கோட்டுருவை முறையாக நிறந்தீட்டத் தேவைப்படும் k இன் மிகச்சிறிய மதிப்பு, கோட்டுருவின் நிற எண் எனப்படும். நிற எண்ணின் குறியீடு $\chi (G)$ ஆகும்.^[2] முறையாக k-நிறந்தீட்டக்கூடிய எண்ணிக்கையை k இன் பல்லுறுப்புக்கோவைச் சார்பாகக் காணலாம். இப்பல்லுறுப்புக்கோவை அக்கலப்புக் கோட்டுருவின் "நிறப் பல்லுறுப்புக்கோவை" என்றழைக்கப்படும்; இதன் குறியீடு $\chi _{G}(k)$ ஆகும்.^[1]