கான்டூர்

[File:Courbe niveau.svg|thumb|right|The bottom part of the diagram shows some contour lines with a straight line running through the location of the maximum value. The curve at the top represents the values along that straight line.]]

A three-dimensional surface, whose contour graph is below.

A two-dimensional contour graph of the three-dimensional surface in the above picture.

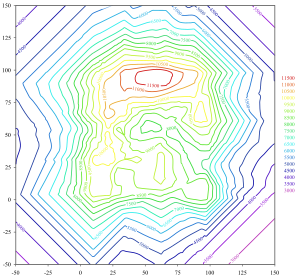
கான்டூர்'

சராசாிக் கடல் மட்டத்திற்கு மேல் ஒரே உயரத்தில் இருக்கும் இடங்களை இணைக்கும் ஒரு கற்பனைக் கோட்டிற்குக் கான்டூர் என்பது பெயர். இதனைச் சம உயரக்கோடு என்றும் கூறலாம். செங்குத்தான சாிவுகளில் கான்டூர்கள் நெருக்கமாக இருக்கும். அதாவது கான்டூர்களுக்கு இடையே உள்ள தூரம் குறைவாக இருக்கும். நிலத்தின் சாிவு குறையக் குறைய கான்டூர்களுக்கு இடையே உள்ள தூரம் அதிகாிக்கும். உயரங்களைச் சர்வே செய்து குறிக்கும் பல புள்ளிகளை மேப்பில் குறிக்கப்படும். அதன்பின் ஒரு குறிப்பிட்ட உயரத்தைக் காட்ட கான்டூர் வரையப்படும். கான்டூர் உயரத்தைக் காட்டும் புள்ளிகள், மற்றப் புள்ளிகளின் உயரத்திற்குத் தக்கவாறு விகிதப்படி குறிக்கப்படுகின்றன. கான்டூர்களின் உயர இடைவெளிகளை (Contour Intervals) இடத்திற்கு jதக்கவாறும் மேப்பின் அளவைக்குத் தக்கவாறும் எடுத்துக்கொள்ள வேண்டும். இந்திய சர்வேக் குழுவினாின் தலப்படங்களில் குறிக்கப்பட்டுள்ள கான்டூர்களின் இடைவெளி 50 அடியாகும். சர்வதேச மேப்புகளில் இவை 250 அடி இடைவெளியில் குறிக்கப்பட்டிருக்கின்றன. சில சமயங்களில் கான்டூர்களுக்கு இடையே உள்ள நிலப்பகுதியை சர்வே செய்யாமல் கற்பனை செய்து சம உயரக்கோடுகள் வரையப்படுகின்றன. அவ்வாறு வரையப்படும் சமஉயரக் கோடுகளுக்கு உருவத் தோற்றக் கோடுகள் (Form-Lines) என்று பெயர்.

கான்டூர்களின் பயன்பாடு

நிலத்தோற்றங்களை மேப்புகளில் குறிப்பதற்கு கான்டூர் முறையே மிகச் சிறந்ததாகும். உலகத்தில் எல்லா நாடுகளும் இம்முறையை கையாளுகின்றன. கான்டூர்களை எளிதில் கண்டுபிடிப்பதற்கு வசதியாக மேப்புகளில் சில குறிப்பிட்ட கான்டூர்களைத் தடித்த கோடுகளாக வரைந்து காட்டுகின்றனர். உதாரணமாக இந்திய இட விவர சர்வே மேப்புகளில் ஒவ்வொரு ஐந்தாவது கான்டூர் கோடு மேற்சொன்ன முறையில் தடித்தவையாக வரையப்பட்டிக்கின்றது.

கான்டூர்களின் மதிப்பு

கான்டூர்களின் மதிப்பை அந்தந்தக் கோடுகளுக்கு மேலேயோ அல்லது இடையேயோ எழுத வேண்டும்.

மேற்கோள்கள்

References

Courant, Richard, Herbert Robbins, and Ian Stewart. What Is Mathematics?: An Elementary Approach to Ideas and Methods. New York: Oxford University Press, 1996. p. 344. Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus : Single and Multivariable (6 ed.). John wiley. பன்னாட்டுத் தரப்புத்தக எண் 978-0470-88861-2. Merriam Webster - contour line contour map Merriam Webster Tracy, John C. Plane Surveying; A Text-Book and Pocket Manual. New York: J. Wiley & Sons, 1907. p. 337.