மாய மாறிலி
ஒரு மாயச் சதுரத்தின் ஒரு நிரை அல்லது ஒரு நிரல் அல்லது ஒரு மூலைவிட்டத்தில் உள்ள எண்களின் கூட்டுத்தொகைள் மூன்றும் ஒரே எண்ணாக இருக்கும். இந்த எண் அம்மாயச் சதுரத்தின் மாய மாறிலி (magic constant) அல்லது மாயக் கூட்டுத்தொகை (magic sum) எனப்படும். எடுத்துக்காட்டாக கீழே தரப்பட்டுள்ள மாயச் சதுரத்தின் மாய மாறிலி 15.
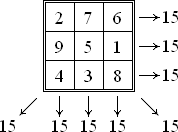
மாயச் சதுரத்துக்கு மட்டுமல்லாது, மாய நட்சத்திரங்கள், மாய கனசதுரங்கள் போன்ற பிற மாய வடிவங்களின் மாய மாறிலிகளுக்கும் இவ்விளக்கம் பொருந்தும்.
மாயச் சதுரங்கள்
தொகு1 முதல் n² வரையிலான எண்களைக் கொண்ட மாயச் சதுரமானது, n -வரிசை மாயச் சதுரம் எனப்படும். இதுவே இயல்பான மாயச் சதுரம் (normal magic square) எனவும் அழைக்கப்படும். இதன் மாய மாறிலியின் மதிப்பு, n -ஐ மட்டுமே சார்ந்திருக்கும்.
மாய மாறிலியின் மதிப்பு:
இவ்வாய்ப்பாடு முதல் k இயல் எண்களின் கூடுதல் காணும் வாய்ப்பாட்டிலிருந்து பெறப்படுகிறது.
முதல் k இயல் எண்களின் கூடுதல் காணும் வாய்ப்பாடு:
இவ்வாய்ப்பாட்டில், k = n² எனப் பிரதியிட:
- n²(n²+1)/2 கிடைக்கிறது.
இது மாயச் சதுரத்தின் மொத்த n நிரைகளில் (நிரல்கள்) உள்ள எண்களின் கூடுதல்.
இம்மதிப்பை n -ஆல் வகுக்கக் கிடைப்பது:
- n(n²+1)/2
இது மாயச் சதுரத்தின் ஒரு நிரையில் (நிரல்) உள்ள எண்களின் கூட்டுத்தொகை. மாயச் சதுரத்தின் ஒவ்வொரு நிரையில் (நிரல் அல்லது மூலைவிட்டம்) உள்ள எண்களின் கூட்டுத்தொகையும் இதே அளவாகவே இருக்கும்.
n = 3, 4, 5, … வரிசை கொண்ட மாயச் சதுரங்களின் மாய மாறிலிகள்: (sequence A006003 in OEIS):
- 15, 34, 65, 111, 175, 260, 369, 505, 671, 870, ….
ஒரு மாயச் சதுரத்தின் ஏதேனும் ஒரு நிரை அல்லது ஒரு நிரல் அல்லது ஒரு மூலைவிட்டத்தில் அமையும் எண்கள் ஒரு மாயத் தொடராக அமையும்.
மாய கனசதுரங்கள்
தொகுஇதேபோல 1, 2, ..., n³ எண்கள் கொண்ட ஒரு மாய கனசதுரத்தின் மாய மாறிலி(OEIS-இல் வரிசை A027441)
மாய நாற்பரிமாண கனசதுரங்கள்
தொகுநான்கு பரிமாணத்தில் அமையும் ஒரு மாய கனசதுரம் (magic tesseract) 1, 2, ..., n4 எண்கள் கொண்டதாய் அமையும்.
இதன் மாய மாறிலி:
பொதுவாக பரிமாணம் d மற்றும் வரிசை n கொண்ட ஒரு மாய மீக்கனசதுரமானது, 1, 2, ..., nd, எண்கள் கொண்டிருக்கும். மேலும் அதன் மாய மாறிலி:
மாய விண்மீன்கள்
தொகுn-முனை கொண்ட ஒரு வழக்கமான மாய விண்மீனின் மாய மாறிலி:
M = 4n + 2.