ஐகன்சு–பிரனெல் கோட்பாடு
ஐகன்சு–பிரனெல் கோட்பாடு (Huygens–Fresnel principle)[1] என்பது அலைப்பரவல் பற்றிய பகுப்பாய்வுக் கொள்கை ஆகும். அலைமுனை ஒன்றில் உள்ள ஒவ்வொரு புள்ளியும் கோள அலைகளின் மூலமாகும் என இது கூறுகிறது. அத்துடன் வெவ்வேறு புள்ளிகளில் இருந்து வெளிப்படும் இரண்டாம் நிலை அலைவரிசைகள் ஒன்றுக்கொன்று குறுக்கிடுகின்றன.[2] இந்தக் கோள அலைவரிசைகளின் கூட்டு புதிய அலைமுனை ஒன்றை உருவாக்குகிறது. எனவே, ஐகன்சு–பிரனெல் கோட்பாடு என்பது தொலைவுப்புல வரம்பு, அருகாமைப்புல விளிம்பு விளைவு மற்றும் எதிரொளிப்பு ஆகியவற்றில் ஒளிரும் அலைப் பரவலின் சிக்கல்களுக்குப் பயன்படுத்தப்படும் பகுப்பாய்வு முறையாகும். டச்சு இயற்பியலாளர் கிறித்தியான் ஐகன்சு, பிரான்சிய இயற்பியலாளர் அகத்தீன்-சான் பிரெனெல் ஆகியோரின் நினைவாக இக்கோட்பாட்டிற்குப் பெயரிடப்பட்டது.

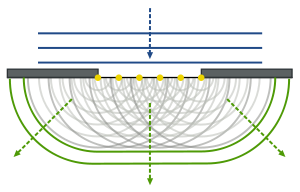
இக் கருத்தியம் அல்லது தத்துவம், முன்னேகும் அலை முகப்பு ஒன்றின் ஒவ்வொரு புள்ளியும் உண்மையில் புதிய குறுக்கீட்டுப் புள்ளியும் புதிய அலைகளுக்கான மூலமுமாக உள்ளது எனக் கொள்கிறது. இந்தக் கருத்தியத்தின்படி, மேலும் ஊடகத்தில் முன்னரே அலை கடந்து வந்த புள்ளிகளிலிருந்து புதிதாக உருவாகி முன்னேறி வரும் எல்லா இரண்டாம் நிலை அலைகளின் தொகுப்பே முன்னேறும் ஒரு முழு அலையாகும். அலை பரப்பல் பற்றிய இக்கருத்துக் கண்ணோட்டம் விளிம்பு விளைவு பல வகை அலை நிகழ்வுகளைப் பற்றிப் புரிந்துகொள்ள உதவுகிறது.
எடுத்துக்காட்டுக்கு, இரண்டு அறைகள் ஒரு பொதுவான திறந்த கதவினால் இணைக்கப்பட்டுள்ளதாகக் கருதுவோம். அதில் ஓர் அறையின் தொலைவிலுள்ள ஒரு மூலையில் ஒலி உண்டாக்கினால் அடுத்த அறையில் உள்ள ஒரு நபருக்கு அந்த ஒலி அந்தக் கதவு இருக்கும் இடத்தில் உருவாக்கிய ஒலி போலவே தோன்றும். இரண்டாம் அறையில் உள்ளவரைப் பொறுத்தமட்டில், கதவினருகில் அதிர்வுக்குள்ளாகும் காற்றே ஒலி மூலமாகும். ஒளி ஒரு தடையின் விளிம்பைக் கடந்து செல்லும் நிகழ்விலும் இதுவே உண்மையாகும். ஆனால் கட்புலனாகும் ஒளியின் அலைநீளம் மிகக் குறைவாக இருப்பதால் இதை உணர முடிவதில்லை.
வரலாறு
தொகு1678 இல், ஐகன்சு ஒளிரும் இடையூறு ஒன்று அடையும் ஒவ்வொரு புள்ளியும் ஒரு கோள அலையின் மூலமாக மாறும் என்று முன்மொழிந்தார்; இந்த இரண்டாம் நிலை அலைகளின் கூட்டு எந்த ஒரு அடுத்தடுத்த நேரத்திலும் அலையின் வடிவத்தை தீர்மானிக்கிறது.[3] இரண்டாம் நிலை அலைகள் "முன்னோக்கிய" திசையில் மட்டுமே பயணம் செய்தன என்று அவர் கருதினார், இது ஏன் என்று அவரது கோட்பாட்டில் விளக்கப்படவில்லை. அவர் நேரியல் மற்றும் கோள அலைப் பரவல் பற்றிய தரமான விளக்கத்தை வழங்கவும், இந்தக் கொள்கையைப் பயன்படுத்தி எதிரொளிப்பு மற்றும் ஒளிமுறிவு விதிகளைப் பெறவும் முடிந்தது. ஆனால் ஒளியின் விளிம்புகள், துளைகள் மற்றும் திரைகள் ஆகியவை பொதுவாக விளிம்பு விளைவு என அழைக்கப்படும் போது ஏற்படும் நேர்கோட்டுப் பரவலில் இருந்து விலகல்களை விளக்க முடியவில்லை.[4] இந்த பிழையின் தீர்வு இறுதியாக 1991 இல் டேவிட் ஏ. பி. மில்லர் என்பவரால் விளக்கப்பட்டது.[5] இதன்படி, ஒளிமூலமானது ஐகன்சு கருதியது போன்று ஒருமுனைவல்ல ஆனால் அது இருமுனைவாகும், இது எதிரொளிப்புத் திசையில் இல்லாதாக்கப்படுகிறது.
1818 இல், பிரெனெல் என்பவர் ஐகன்சின் கொள்கையானது, தனது சொந்தக் குறுக்கீடுக் கொள்கையுடன் ஒளியின் நேர்கோட்டுப் பரவலையும் விளிம்பு விளைவுகளையும் விளக்க முடியும் என்பதைக் காட்டினார்.[6] பரிசோதனை முடிவுகளுடன் இதற்கான உடன்பாட்டைப் பெற, அவர் இரண்டாம் நிலை அலைகளின் கட்டம் (அவத்தை), வீச்சு, ஒரு சரிவுக் காரணி பற்றிய கூடுதல் தன்னெண்ண அனுமானங்களைச் சேர்க்க வேண்டியிருந்தது. இந்த அனுமானங்களுக்கு வெளிப்படையான இயற்பியல் அடித்தளம் இல்லை ஆனாலும் இது புவசோனின் புள்ளி[7] உட்பட்ட பல சோதனை அவதானிப்புகளுடன் ஒத்துப்போகும் கணிப்புகளுக்கு வழிவகுத்தது.
அலைகம்பக் கோட்பாட்டிலும், பொறியியலிலும், தற்போதைய மூலங்களை கதிர்வீச்சு செய்வதற்கான ஐகன்சு-பிரனெல் கொள்கையின் மறுசீரமைப்பு மேற்பரப்பு சமநிலைக் கொள்கை என அறியப்படுகிறது.[8][9]
கோட்பாட்டின் கணித வெளிப்பாடு
தொகுஅதிர்வெண் f இல் அதிர்வுறும் P0 என்ற புள்ளியில் அமைந்துள்ள புள்ளி மூலத்தைக் கவனிப்போம். சிக்கல் வீச்சு எனப்படும் கலப்பு மாறி U0 மூலம் இந்நிகழ்வு விவரிக்கப்படலாம். இது அலைநீளம் λ, அலைஎண் k = 2π/λ உடன் ஒரு கோள அலையை உருவாக்குகிறது. விகிதாச்சாரத்தின் மாறிலிக்குள், P0 இலிருந்து r0 தொலைவில் அமைந்துள்ள Q புள்ளியில் முதன்மை அலையின் சிக்கல் வீச்சு:
பயணித்த தூரத்திற்கு தலைகீழ் விகிதத்தில் வீச்சு குறைகிறது, மேலும் கட்டமானது பயணித்த தூரத்தின் k மடங்குகளாக மாறுகிறது.
ஐகன்சின் கோட்பாடு, அலைகளின் மேற்பொருத்துகைக் கொள்கை ஆகியவற்றைப் பயன்படுத்தி, r0 ஐக் கொண்டுள்ள கோளத்தின் ஒவ்வொரு புள்ளியிலிருந்தும் பங்களிப்புகளைச் சுருக்கி, மேலும் ஒரு புள்ளி P இல் சிக்கல் அலைவீச்சு கண்டறியப்படுகிறது. சோதனை முடிவுகளுடன் உடன்பாட்டைப் பெறுவதற்காக, கோளத்தில் உள்ள இரண்டாம் நிலை அலைகளின் தனிப்பட்ட பங்களிப்புகள் −i/λ என்ற மாறிலியாலும், K(χ) என்ற கூடுதல் சாய்வு காரணியாலும் பெருக்கப்பட வேண்டும் என்று பிரனெல் கண்டறிந்தார். முதல் தற்கோளின் பொருள் என்னவெனில், இரண்டாம் நிலை அலைகள் முதன்மை அலைக்கு ஒரு முழுச் சுழற்சியின் கால் பகுதி அளவு கட்ட ஒவ்வாமையாக ஊசலாடுகின்றன, அத்துடன் இரண்டாம் நிலை அலைகளின் அளவு முதன்மை அலைக்கு 1:λ என்ற விகிதத்தில் இருக்கும். χ = 0 ஆக இருக்கும் போது K(χ) அதிகபட்ச மதிப்பைக் கொண்டிருந்தது என்றும், χ = π/2 ஆக இருக்கும் போது சுழியத்திற்குச் சமமாக இருக்கும் என்றும் அவர் கருதினார், இங்கு χ என்பது முதன்மை அலைகத்திற்கும் இரண்டாம் நிலை அலைமுகத்திற்கும் இடையே உள்ள கோணமாகும். இரண்டாம் நிலை அலைகளின் பங்களிப்பின் காரணமாக P இல் உள்ள சிக்கல் வீச்சு பின்வருவனவற்றால் வழங்கப்படுகிறது:[10]
இங்கு, S என்பது கோளத்தின் மேற்பரப்பை விவரிக்கிறது, s என்பது Q, P' ஆகிய புள்ளிகளுக்கிடையேயான உள்ள தூரம்.
வெவ்வேறு வலயங்களுக்கான தோராயமான K இன் மதிப்புகளைக் கண்டறிய பிரனெல் ஒரு வலயக் கட்டுமான முறையைப் பயன்படுத்தினார்,[7] இது பரிசோதனை முடிவுகளுடன் ஒத்துப்போகும் கணிப்புகளைச் செய்ய அவருக்கு உதவியது. கிர்க்காஃபின் தொகையீட்டுத் தேற்றம் ஐகன்சு-பிரனெல் கோட்பாட்டின் அடிப்படை யோசனையை உள்ளடக்கியது.[7]
ஒற்றை விரிவடையும் கோள அலையை உள்ளடக்கிய ஒரு துளை வெளிச்சத்திற்கு, அலையின் வளைவின் ஆரம் போதுமானதாக இருந்தால், கிர்க்காஃப் K (χ) க்கு பின்வரும் சமன்பாட்டைக் கொடுத்தார்:[7]
ஐகன்சு-பிரனெல் கோட்பாட்டின்படி K இன் அதிகபட்ச மதிப்பு χ = 0 இல் உள்ளது; இருப்பினும், K இன் மதிப்பு χ = π/2 இல் சுழியமாக இல்லை, ஆனால் χ = π இல் அது சுழியமாக உள்ளது.
மேலே தரப்பட்டுள்ள K(χ) என்பதன் சமன்பாடு, வளைவின் போதுமான பெரிய ஆரம் கொண்ட ஒற்றைக் கோள அலையால் விளிம்புவிளைவை ஏற்படுத்தும் துளை ஒளிர்வூட்டப்படுகிறது என்று கருதப்பட்டது.[10] ஒரு தன்னிச்சையாக ஒளிரும் வெளிச்சத்தை புள்ளி மூலங்களின் தொகுப்பாக சிதைக்க முடியும், அத்துடன் ஒவ்வொரு புள்ளி மூலத்திற்கும் தனித்தனியாகக் கொள்கையைப் பயன்படுத்த அலை சமன்பாட்டின் நேர்கோட்டுத்தன்மையை செயல்படுத்தலாம். K(χ) பொதுவாக இவ்வாறு தரப்படலாம்:[10]
இங்கு, K மேலே கூறப்பட்ட நிபந்தனைகளைப் பூர்த்தி செய்கிறது (χ = 0 இல் அதிகபட்ச மதிப்பு, χ = π/2 இல் சுழியம்).
மேற்கோள்கள்
தொகு- ↑ Longhurst RS, Geometrical and Physical Optics, 2nd Edition, 1968, Longmans [London]
- ↑ "Huygens' Principle". MathPages. பார்க்கப்பட்ட நாள் 2017-10-03.
- ↑ Chr. Huygens, Traité de la Lumière (drafted 1678; published in Leyden by Van der Aa, 1690), translated by Silvanus P. Thompson as Treatise on Light (London: Macmillan, 1912; Project Gutenberg edition, 2005), p.19.
- ↑ Heavens, O. S.; Ditchburn, R. W. (1987). Insight into Optics. Chichester: Wiley & Sons. பன்னாட்டுத் தரப்புத்தக எண் 0-471-92769-4.
- ↑ Miller, David A. B. (1991). "Huygens's wave propagation principle corrected". Optics Letters 16 (18): 1370–1372. doi:10.1364/OL.16.001370. பப்மெட்:19776972. Bibcode: 1991OptL...16.1370M. https://semanticscholar.org/paper/0dd2d800622bbcf22472c1c8042f11d390bb9ea5.
- ↑ A. Fresnel, "Mémoire sur la diffraction de la lumière" (deposited 1818, "crowned" 1819), in Oeuvres complètes (Paris: Imprimerie impériale, 1866–70), vol.1, pp. 247–363; partly translated as "Fresnel's prize memoir on the diffraction of light", in H. Crew (ed.), The Wave Theory of Light: Memoirs by Huygens, Young and Fresnel, American Book Co., 1900, pp. 81–144. (Not to be confused with the earlier work of the same title in Annales de Chimie et de Physique, 1:238–81, 1816.)
- ↑ 7.0 7.1 7.2 7.3 Born, Max; Wolf, Emil (1999). Principles of Optics. Cambridge University Press. பன்னாட்டுத் தரப்புத்தக எண் 978-0-521-64222-4.
- ↑ Balanis, Constantine A. (2012). Advanced Engineering Electromagnetics. John Wiley & Sons. pp. 328–331. பன்னாட்டுத் தரப்புத்தக எண் 978-0-470-58948-9.
- ↑ Balanis, Constantine A. (2005). Antenna Theory: Analysis and Design (3rd ed.). John Wiley and Sons. p. 333. பன்னாட்டுத் தரப்புத்தக எண் 047166782X.
- ↑ 10.0 10.1 10.2 J. Goodman (2005). Introduction to Fourier Optics (3rd ed.). Roberts & Co Publishers. பன்னாட்டுத் தரப்புத்தக எண் 978-0-9747077-2-3.
வெளி இணைப்புகள்
தொகு- Huygens' Principle at MathPages