சமதொடுகோட்டு அச்சு

ஒரு புள்ளியிலிருந்து இரு வட்டங்களுக்கு வரைப்படும் தொடுகோடுகள் சமநீளமுள்ளவையாக இருக்குமாறு இயங்கும் புள்ளியின் இயங்குவரை ஒரு நேர்கோடாக அமையும். இக்கோடு அவ்விருவட்டங்களின் சமதொடுகோட்டு அச்சு (radical axis) என அழைக்கப்படுகிறது. சமதொடுகோட்டு அச்சின் மீதமையும் எந்தவொரு புள்ளி P -ஐயும் மையமாகக் கொண்டு வரையப்படும் வட்டம் எடுத்துக்கொள்ளப்பட்ட இரு வட்டங்களையும் செங்குத்தாக வெட்டும். சமதொடுகோட்டு அச்சின் மீதமையும் ஒவ்வொரு புள்ளிக்கும் இவ்வாறு அமையும் வட்டம் தனித்ததொன்றாகும். மறுதலையாக, இருவட்டங்களுக்கும் செங்குத்து வட்டமாக அமையும் வட்டத்தின் மையம் அவ்விருவட்டங்களின் சமதொடுகோட்டு அச்சின் மீதமையும். சமதொடுகோட்டு அச்சின் மீதுள்ள புள்ளியிலிருந்து இரு வட்டங்களுக்கும் வரையப்படும் தொடுகோடுகள் சமநீளமுடையவை என்பதால், சமதொடுகோட்டு அச்சின் மீதமையும் ஒவ்வொரு புள்ளியின் படியும் அவ்விரு வட்டங்களைப் பொறுத்து சமம் எனலாம்.

இரு வெட்டிக்கொள்ளாத வட்டங்களின் (தடித்த கருப்பு) சமதொடுகோட்டு அச்சு சிவப்புக் கோடு. சமதொடுகோட்டு அச்சின் மீதுள்ள புள்ளியை (நீலம்) மையமாகவும் அப்புள்ளியிலிருந்து இரு வட்டங்களுக்கு வரையப்பட்ட சமதொடுகோட்டு நீளத்தை (நீல நிறக் கோடுகள்) ஆரமாகவும் கொண்டு வரையப்பட்ட வட்டம் (இடையிட்ட தோற்றம்) எடுத்துக்கொண்ட இரு வட்டங்களுக்குச் செங்குத்து வட்டமாக அமையும்.

இரு வெட்டிக்கொள்ளும் வட்டங்களின் சமதொடுகோட்டு அச்சானது வட்டங்கள் வெட்டிக்கொள்ளும் புள்ளிகளை இணைக்கும் பொது நாணாக அமையும் வெட்டுக்கோடாகும்.

$R^{2}=d_{1}^{2}-r_{1}^{2}=d_{2}^{2}-r_{2}^{2}$

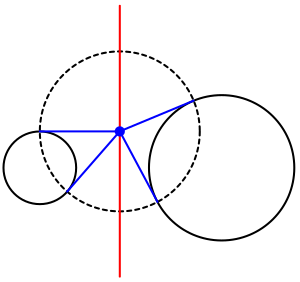
இங்கு,

r₁, r₂ -வட்டங்களின் ஆரங்கள்;

d₁, d₂ -புள்ளி P -க்கும் வட்டங்களின் மையங்களுக்கும் இடைப்பட்ட தொலைவு;

R -P ஐ மையமாகக் கொண்ட செங்குத்து வட்டத்தின் ஆரம்.

சமதொடுகோட்டு அச்சு எப்பொழுதும் ஒரு நேர்கோடாகவும் எடுத்துக்கொள்ளப்பட்ட வட்டங்களின் மையங்களை இணைக்கும் கோட்டிற்கு செங்குத்தாகவும் அமையும். வெட்டிக்கொள்ளாத வட்டங்களின் சமதொடுகோட்டு அச்சானது, இரண்டில் பெரியதாகவுள்ள வட்டத்திற்கு அருகில் இருக்கும். இரண்டு வட்டங்களும் வெட்டும் வட்டங்கள் எனில் சமதொடுகோட்டு அச்சு அவை வெட்டும் புள்ளிகளின் வழியே செல்லும். இரண்டு வட்டங்களும் தொடுவட்டங்கள் எனில் சமதொடுகோட்டு அச்சு அவ்வட்டங்களுக்குப் பொதுத் தொடுகோடாக இருக்கும். ஒரே கோட்டின் மீதமைந்த மையங்களையும், ஒரே கோட்டை சமதொடுகோட்டு அச்சாகவும் கொண்ட வட்டங்கள் அனைத்தும் பொதுஅச்சு வட்டங்களின் கற்றை எனப்படும்.

சமதொடுகோட்டச்சுச் சந்தி

எடுத்துக்கொள்ளப்பட்ட மூன்று வட்டங்களின் (கருப்பு) சமதொடுகோட்டு அச்சுகள் (நீலம்) சந்திக்கும் புள்ளியான சமதொடுகோட்டச்சுச் சந்தியை (ஆரஞ்சு) மையமாகக் கொண்டு வரையப்பட்ட தனித்ததொரு வட்டமானது (ஆரஞ்சு) முதல் மூன்று வட்டங்களின் செங்குத்து வட்டமாகும்.

எந்த இரண்டும் பொதுமைய வட்டங்களாக இல்லாத மூன்று வட்டங்கள் A, B , C .

இம்மூன்று வட்டங்களில் இரண்டிரண்டாக வட்டங்களை எடுத்துக்கொண்டு அவற்றின் சமதொடுகோட்டு அச்சுகள் காண, அம்மூன்று அச்சுகளும் ஒரே புள்ளியில் சந்திக்கலாம் அல்லது இணையாகவும் இருக்கலாம். அவை மூன்றும் சந்திக்குமானால் சந்திக்கும் புள்ளியானது மூன்று வட்டங்களின் சமதொடுகோட்டச்சுச் சந்தி எனப்படும். மூன்று சமதொடுகோட்டு அச்சுகளும் இணையாக இருந்தால் அவை முடிவிலியில் சந்திக்கும்.

இம்மூன்று வட்டங்களின் சமதொடுகோட்டு அச்சுகளும் ஒரு புள்ளியில் சந்திக்கும் என்பதை எளிதாக விளக்கலாம்:

மூன்று வட்டங்களில் இரண்டிரண்டாக எடுத்துக் கொண்டு சமதொடுகோட்டு அச்சுகளைக் காண, ஒவ்வொரு சோடி வட்டத்தின் சமதொடுகோட்டு அச்சிலிருந்தும் அவ்வட்டங்களுக்கு வரையப்படும் தொடுகோடுகள் சமநீளமுள்ளவையாக இருக்கும். எனவே கடப்பு உறவின் படி (transitive relation), மூன்றுவட்டங்களுக்கும் வரையப்படும் தொடுகோடுகள் மூன்றும் சமநீளமுள்ளவையாக உள்ளவாறு, மூன்று சமதொடுகோட்டு அச்சுகளுக்கும் பொதுவான ஒரு புள்ளி இருக்கும். இப்பொதுப் புள்ளியே சமதொடுகோட்டச்சுச் சந்தியாகும்.

சமதொடுகோட்டச்சுச் சந்தியை மையமாகவும், சமதொடுகோட்டு நீளத்தை ஆரமாகவும் கொண்டு வரையப்படும் வட்டமானது எடுத்துக்கொள்ளப்பட்ட மூன்று வட்டங்களுக்கும் செங்குத்து வட்டமாக இருக்கும். அவ்வாறு அமையக்கூடிய வட்டம் தனித்ததொன்றாகும். மேலும் அது தரப்பட்ட மூன்று வட்டங்களின் சமதொடுகோட்டு வட்டம் என்றழைக்கப்படும்.

வரைதல்

சமதொடுகோட்டு அச்சு வரைதல்

• எடுத்துக்கொள்ளப்பட்ட இரு வட்டங்களின் மையங்களை (B , V) இணைக்கும் கோட்டிற்கு (நீலம்), சமதொடுகோட்டு அச்சு (சிவப்பு) செங்குத்தாக இருக்கும். இவ்விரண்டு கோடுகளும் சந்திக்கும் புள்ளி K.
• K இலிருந்து B , V -க்குள்ள தொலைவு x₁ , x₂.
• B , V -க்கு இடையேயுள்ள தொலைவு x₁+x₂ = D.
• சமதொடுகோட்டு அச்சின் மீதமையும் ஒரு புள்ளி J -க்கும் B , V -க்கும் இடையேயுள்ள தொலைவுகள் முறையே d₁, d₂.
• இரு வட்டங்களின் ஆரங்கள், r₁, r₂
• J , K -க்கும் இடையேயுள்ள தொலைவு L.

J , சமதொடுகோட்டு அச்சின் மீதுள்ளதால் இரு வட்டங்களைப் பொறுத்த அதன் படிகள் சமமாகும்:

$d_{1}^{2}-r_{1}^{2}=d_{2}^{2}-r_{2}^{2}$

பித்தாகரசு தேற்றப்படி,

$d_{1}^{2}=L^{2}+x_{1}^{2}$

$d_{2}^{2}=L^{2}+x_{2}^{2}$

d₁, d₂ மதிப்புகளைப் பிரதியிட,

$\Rightarrow L^{2}+x_{1}^{2}-r_{1}^{2}=L^{2}+x_{2}^{2}-r_{2}^{2}$

$\Rightarrow x_{1}^{2}-x_{2}^{2}=r_{1}^{2}-r_{2}^{2}$

இருபுறமும் D = x₁+x₂ ஆல் வகுக்க,

$\Rightarrow x_{1}-x_{2}={\frac {r_{1}^{2}-r_{2}^{2}}{D}}$

இதனுடன் $x_{1}+x_{2}=D$சமன்பாட்டைக் கூட்ட,

$\Rightarrow 2x_{1}=D+{\frac {r_{1}^{2}-r_{2}^{2}}{D}}$ மதிப்பும், கழிக்க,

$\Rightarrow 2x_{2}=D-{\frac {r_{1}^{2}-r_{2}^{2}}{D}}$ மதிப்பும் கிடைக்கிறது.

x₁ அல்லது x₂ இன் மதிப்பைக் கொண்டு வட்டங்களின் மையங்களை இணைக்கும் கோட்டுத்துண்டின் மீது புள்ளி K ஐக் குறித்துக் கொண்டு அதன் வழியே மையங்களை இணைக்கும் கோட்டுத்துண்டிற்கு செங்குத்து வரைய அச்செங்குத்துக் கோடு எடுத்துக்கொண்ட இரு வட்டங்களின் சமதொடுகோட்டு அச்சாகும்.

முந்நேரியல் ஆயதொலைவுகளில் சமதொடுகோட்டச்சுச் சந்தி

வட்டங்கள் முந்நேரியல் ஆயதொலைவுகளில் தரப்பட்டிருந்தால் சமதொடுகோட்டச்சுச் சந்தி அணிக்கோவை வடிவில் தரப்படுகிறது.

X = x : y : z என்பது முக்கோணம் ABC இன் தளத்திலமையும் ஏதேனும் ஒரு புள்ளி. முக்கோணத்தின் பக்க நீளங்கள், a = |BC|, b = |CA|, c = |AB|.

வட்டங்கள் பின்வருமாறு தரப்படுகின்றன:

(dx + ey + fz)(ax + by + cz) + g(ayz + bzx + cxy) = 0

(hx + iy + jz)(ax + by + cz) + k(ayz + bzx + cxy) = 0

(lx + my + nz)(ax + by + cz) + p(ayz + bzx + cxy) = 0

இப்பொழுது சமதொடுகோட்டச்சுச் சந்தி அணிக்கோவையாக:

$\det {\begin{bmatrix}g&k&p\\e&i&m\\f&j&n\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\f&j&n\\d&h&l\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\d&h&l\\e&i&m\end{bmatrix}}.$

ஆதாரங்கள்

• Johnson RA (1960). Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle (reprint of 1929 edition by Houghton Miflin ed.). New York: Dover Publications. pp. 31–43. பன்னாட்டுத் தரப்புத்தக எண் 978-0-486-46237-0.

மேலும் தெரிந்துகொள்ள

• Ogilvy CS (1990). Excursions in Geometry. Dover. pp. 17–23. பன்னாட்டுத் தரப்புத்தக எண் 0-486-26530-7.
• Coxeter HSM, Greitzer SL (1967). Geometry Revisited. Washington: MAA. pp. 31–36, 160–161. பன்னாட்டுத் தரப்புத்தக எண் 978-0-88385-619-2.
• Clark Kimberling, "Triangle Centers and Central Triangles," Congressus Numerantium 129 (1998) i–xxv, 1–295.

வெளி இணைப்புகள்

விக்கிமீடியா பொதுவகத்தில்,
Radical axes
என்பதில் ஊடகங்கள் உள்ளன.

• Weisstein, Eric W., "Radical line", MathWorld.
• Weisstein, Eric W., "Chordal theorem", MathWorld.
• Animation at Cut-the-knot