மீப்பெரு முழுஎண் சார்பு

கணிதத்தில் மீப்பெரு முழுஎண் சார்பு (greatest integer function) என்பது மெய்யெண்களின் மீது வரையறுக்கப்பட்டதொரு சார்பு. இச்சார்பின் கீழ் ஒரு மெய்யெண்ணின் சார்பலன் அம்மெய்யெண்ணை விட சிறிய முழுஎண்களுக்குள் மிகப்பெரிய முழுஎண்ணாகும். கீழ்மட்டச் சார்பு (floor function) எனவும் இச்சார்பு அழைக்கப்படுகிறது. இதன் குறியீடு $\lfloor x\rfloor .$

மீப்பெரு முழுஎண் சார்பின் வரைபடம்

எடுத்துக்காட்டுகள்:

• $\lfloor {\frac {12}{5}}\rfloor$ = $\lfloor 2.4\rfloor =2$
• $\lfloor 2\rfloor =2$
• $\lfloor -2\rfloor =-2$
• $\lfloor -2.7\rfloor =-3$

குறியீடு

கார்ல் ஃப்ரெடெரிக் காஸ் இருபடி நேர்எதிர்மை -குறித்த தனது மூன்றாவது நிறுவலில் (1808) மீப்பெரு முழுஎண் சார்புக்கு சதுர அடைப்புக் குறியீட்டைப் ($[x]$) பயன்படுத்தினார் கென்னத் இ. ஐவர்சன் 1962 ஆம் ஆண்டு மீப்பெரு முழுஎண் சார்பு மற்றும் மீச்சிறு முழுஎண் சார்பு ஆகிய இரு சார்புகளையும், மற்றும் அவற்றின் குறியீடுகளாக முறையே$\lfloor x\rfloor ,$ $\lceil x\rceil$ ஆகிய இரண்டையும் அறிமுகப்படுத்தும்வரை இக்குறியீடே பயன்படுத்தப்பட்டு வந்தது. தற்போது இருவிதமான குறியீடுகளும் பயன்படுத்தப்படுகின்றன.

வரையறையும் பண்புகளும்

மீப்பெரு முழுஎண் சார்பு பின்வருமாறு வரையறுக்கப்படுகிறது:

$\lfloor x\rfloor =\max \,\{m\in \mathbb {Z} \mid m\leq x\}\,$

ஓரலகு நீளமுள்ள பாதி திறந்த இடைவெளியில் ஒரேயொரு முழுஎண் மட்டுமே இருக்கும் என்பதால், x என்ற மெய்யெண்ணுக்கு,

$x-1<m\leq x\leq n<x+1.\;$

என்றவாறு m , n என இரு தனித்த முழுஎண்கள் அமைகின்றன. இதனைப் பயன்படுத்தி மீப்பெரு முழுஎண் சார்பின் வரையறையைப் பின்வருமாறும் கூறலாம்:

$\lfloor x\rfloor =m\,$

• $\lfloor x+n\rfloor =\lfloor x\rfloor +n\,$ (n ஒரு முழு எண்)
• $\lfloor x\rfloor +\lfloor y\rfloor \leq \lfloor x+y\rfloor \leq \lfloor x\rfloor +\lfloor y\rfloor +1\,$ (x, y இரு மெய்யெண்கள்)
• ${\Big \lfloor }\lfloor x\rfloor {\Big \rfloor }=\lfloor x\rfloor \,$ (மீப்பெரு முழுஎண் சார்பு ஒரு தன்னடுக்குச் சார்பு

மீச்சிறு முழுஎண் சார்புடன் தொடர்பு

• $\lfloor x\rfloor \leq \lceil x\rceil \,$

x முழு எண்ணாக இருந்தால், இருந்தால் மட்டுமே, இதில் சமக்குறி உண்மையாகும். அதாவது:

$\lceil x\rceil -\lfloor x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} \end{cases}}\,$

• ${\begin{aligned}\lfloor x\rfloor +\lceil -x\rceil &=0\\-\lfloor x\rfloor &=\lceil -x\rceil \\-\lceil x\rceil &=\lfloor -x\rfloor \end{aligned}}\,$

• $\lfloor x\rfloor +\lfloor -x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\-1&{\mbox{ if }}x\not \in \mathbb {Z} ,\end{cases}}\,$

• $\lceil x\rceil +\lceil -x\rceil ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} .\end{cases}}\,$

தொடர்ச்சி

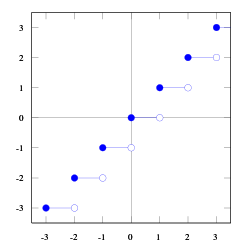
மீப்பெரு முழுஎண் சார்பு தொடர்ச்சியான சார்பல்ல; எனினும் அது மேல் அரைத்தொடர்ச்சியானதாகவும் துண்டுவாரி மாறிலிச் சார்பாகவும் அமையும். கட்டுரையின் தொடக்கத்தில் தரப்பட்டுள்ள வரைபடத்திலிருந்து இவ் விவரத்தைக் காணலாம்.

வெளி இணைப்புகள்

விக்கிமீடியா பொதுவகத்தில்,
மீப்பெரு மற்றும் மீச்சிறு சார்புகள்
என்பதில் ஊடகங்கள் உள்ளன.

• Hazewinkel, Michiel, ed. (2001), "Floor function", Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104
• Štefan Porubský, "Integer rounding functions", Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, retrieved 24 October 2008
• Weisstein, Eric W., "Floor Function", MathWorld.
• Weisstein, Eric W., "Ceiling Function", MathWorld.