ஆற்றல்மிகு எண்

ஆற்றல்மிகு எண் (powerful number) என்பது, ஒரு பகா எண்ணையும் அப்பகாஎண்ணின் வர்க்கத்தையும் வகுஎண்களாகக் கொண்ட நேர் முழு எண் ஆகும். அதாவது m என்ற நேர் முழுஎண் ஆற்றல்மிகு எண் எனில், அதனை வகுக்கும் ஒவ்வொரு பகாஎண் p க்கும், p²ம் m ஐ வகுக்கும்.

குசேனைரே கோல்கள் மூலம் 1, 4, 8, 9 ஆகியவை ஆற்றல்மிகு எண்களென விளக்கும் படம்.

இதற்குச் சமானமாக, ஒரு ஆற்றல்மிகு எண்ணானது, ஒரு வர்க்க எண் மற்றும் ஒரு கன எண்ணின் பெருக்கமாக அமையும் எனவும் வரையறுக்கப்படுகிறது. அதாவது, ஆற்றல்மிகு எண் m

m = a²b³, (a, b நேர் முழுஎண்கள்) வடிவில் அமையும்.

எடுத்துக்காட்டுகள்:

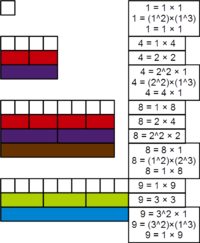
• 4 இன் பகாக்காரணி 2 மற்றும் அதன் வர்க்கம் 4=2² இரண்டுமே நான்கின் வகுஎண்களாக உள்ளதால் 4 ஒரு ஆற்றல்மிகு எண்.
• பகாக்காரணிகள் 2, 3 ம் மற்றும் அவற்றின் வர்க்கங்கள் 4=2², 9=3² நான்குமே 36இன் வகுஎண்களாக உள்ளதால் 36 ஒரு ஆற்றல்மிகு எண்.

இரண்டாவது வரையறைப்படி, ஆற்றல்மிகு எண்ணின் பொதுவடிவம்:

m =a²b³, ( a, b நேர் முழுஎண்கள்)

4 = 2² x 1³

36 = 6² x 1³

200= 25 x 8 = 5² x 2³

1 முதல் 1000 வரையுள்ள ஆற்றல்மிகு எண்களின் பட்டியல்:

1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400, 432, 441, 484, 500, 512, 529, 576, 625, 648, 675, 676, 729, 784, 800, 841, 864, 900, 961, 968, 972, 1000 (OEIS-இல் வரிசை A001694)

.

இரு வரையறைகளின் சமானத்தன்மை

${\begin{aligned}144000&=2^{7}\times 3^{2}\times 5^{3}\\&=2^{3}\times 2^{4}\times 3^{2}\times 5^{3}\\&=(2\times 5)^{3}\times (2^{2}\times 3)^{2}\end{aligned}}$

144000, ஒரு வலுவான எண்.
இதன் பகாக் கரணிகளின் ஒவ்வொன்றின் அடுக்கும் '1'விடப் பெரியது.
ஒரு வர்க்கம் மற்றுமொரு கனத்தின் பெருக்கலாகவுள்ளது.

m = a²b³ எனில்

• a இன் ஒவ்வொரு பகாக்காரணியும் m இன் பகாக்காரணியாக்கத்தில் குறைந்தபட்சம் 2 அடுக்கினைக் கொண்டிருக்கும்;
• அதேபோல b இன் ஒவ்வொரு பகாக்காரணியும் m இன் பகாக்காரணியாக்கத்தில் குறைந்தபட்சம் 3 அடுக்கினைக் கொண்டிருக்கும்;
• இதிலிருந்து m இன் ஒவ்வொரு பகாக்காரணியும் குறைந்தபட்சம் அடுக்கு 2ஐக் கொண்டிருக்கும் என அறியலாம். அதாவது m ஐ வகுக்கும் ஒவ்வொரு பகாஎண்ணின் வர்க்கமும் m ஐ வகுக்கும், எனவே m ஒரு ஆற்றல்மிகு எண்ணாகிறது.

144000 = 12² x 10³

12 இன் பகாக்காரணியாக்கம் = 2² x 3

10 இன் பகாக்காரணியாக்கம் = 2 x 5

144000 இன் பகாக்காரணியாக்கம் =2⁷ x 3² x 5³

14400 இன் பகாக்காரணிகளான 2, 3, 5 இன் வர்க்கங்களும் அதன் காரணிகளாக உள்ளன; அதாவது 144000ஐ வகுக்கும் ஒவ்வொரு பகாஎண்ணின் வர்க்கமும் 144000ஐ வகுக்கும் என்பதால் 12² x 10³ வடிவிலமையும் 144000 ஒரு ஆற்றல்மிகு எண்ணாகிறது

m ஆற்றல்மிகு எண் எனில்

m இன் பகாக்காரணியாக்கம்:

$m=\prod p_{i}^{\alpha _{i}},$ , α_i ≥ 2

α_i ஒற்றையெண் எனில் γ_i = 3 எனவும் மற்றபடி γ_i = 0 எனவும்,

$\beta _{i}=\alpha _{i}-\gamma _{i}$ எனவும் வரையறுத்தால், β_i இன் மதிப்புகள் அனைத்தும் எதிரில்லா இரட்டை முழுஎண்களாக இருக்கும்.

$m=\prod p_{i}^{\alpha _{i}}=\prod p_{i}^{\beta _{i}+\gamma _{i}}=(\prod p_{i}^{\beta _{i}})(\prod p_{i}^{\gamma _{i}})=(\prod p_{i}^{\beta _{i}/2})^{2}(\prod p_{i}^{\gamma _{i}/3})^{3}$

எனவே ஆற்றல்மிகு எண்ணான m , ஒரு வர்க்கஎண் மற்றும் கனஎண்ணின் பெருக்க வடிவிலுள்ளது.

எனவே இருவிதமான வரையறைகளின் சமானத்தன்மை நிறுவப்படுகிறது.

அடுத்தடுத்த எண்களாய் அமையும் ஆற்றல்மிகு எண்சோடிகள்

அடுத்தடுத்த எண்களாய் அமையும் ஆற்றல்மிகு எண்சோடிகள்:

(8, 9), (288, 289), (675, 676), (9800, 9801), ... (Sloane's A060355 and A118893)

x² − 8y² = 1 என்ற பெல்லின் சமன்பாட்டிற்கு முடிவிலா முழுஎண்கள் தீர்வுகள் இருப்பதால், அடுத்தடுத்த ஆற்றல்மிகு எண்சோடிகளும் முடிவிலா எண்ணிக்கையில் உள்ளன (Golomb, 1970). மேலும் பொதுவாக,

x² − ny² = ±1 (n ஏதேனுமொரு கனஎண்) என்ற பெல்லின் சமன்பாட்டினைத் தீர்ப்பதன் மூலம் ஆற்றல்மிகு எண்சோடிகளைக் காணலாம். இவ்வாறு பெறப்படும் ஒவ்வொரு ஆற்றல்மிகு எண்சோடியிலும் ஒரு எண் முழுவர்க்கமாக இருக்கும்.

இரண்டில் எந்த எண்ணும் முழுவர்க்க எண்ணாக இல்லாத ஆற்றல்மிகு எண்சோடிகள் (23³, 2³3²13²) முடிவிலா எண்ணைக்கையில் உள்ளனவா என்ற கேள்வி கணிதவியலாளர் ஏர்டோசுவால் எழுப்பப்பட்டு, 3³c²+1=7³d² என்ற சமன்பாட்டின் முடிவிலா எண்ணிக்கையிலான தீர்வுகள் அவ்வாறு அமைகின்றன என கணிதவியலாளர் ஜாரொஸ்லா வ்ரொபிலெஸ்கியால் (Jaroslaw Wroblewski)) நிறுவப்பட்டது. அடுத்தடுத்தமையும் தொடர்ச்சியான மூன்று ஆற்றல்மிகு எண்கள் கிடையாதென கணிதவியலாளர்களான ஏர்டோசு, மோலின், வால்ஷ் ஆகியோரின் அனுமானம் கூறுகிறது.

பொதுமைப்படுத்தல்

ஒரு நேர் முழுஎண்ணின் அனைத்துப் பகாஎண்காரணிகளும் குறைந்தபட்சம் k அடுக்குடையதாய் இருந்தால் அந்த எண் k-ஆற்றல்மிகு எண் (k-powerful number, k-ful number, k-full number) என்றழைக்கப்படும்.

(2^k+1 − 1)^k,  2^k(2^k+1 − 1)^k,   (2^k+1 − 1)^k+1-இவை மூன்றும் கூட்டுத் தொடர்வரிசையில் அமையும் k-ஆற்றல்மிகு எண்கள் ஆகும்.

a₁, a₂, ..., a_s என்பவை கூட்டுத் தொடரில் அமையும் k-ஆற்றல்மிகு எண்கள். இத்தொடரின் பொதுவித்தியாசம் d எனில்:

a₁(a_s + d)^k,   

a₂(a_s + d)^k, ..., a_s(a_s + d)^k, (a_s + d)^k+1

ஆகிய s + 1 எண்கள் கூட்டுத் தொடரில் அமையும் k-ஆற்றல்மிகு எண்கள் ஆகும்.

மேற்கோள்கள்

• Cohn, J. H. E. (1998). "A conjecture of Erdős on 3-powerful numbers". Math. Comp. 67 (221): 439–440. doi:10.1090/S0025-5718-98-00881-3. http://www.ams.org/mcom/1998-67-221/S0025-5718-98-00881-3/. 
• Paul Erdős and George Szekeres (1934). "Über die Anzahl der Abelschen Gruppen gegebener Ordnung und über ein verwandtes zahlentheoretisches Problem". Acta Litt. Sci. Szeged 7: 95–102. 
• Solomon W. Golomb (1970). "Powerful numbers". American Mathematical Monthly 77 (8): 848–852. doi:10.2307/2317020. https://archive.org/details/sim_american-mathematical-monthly_1970-10_77_8/page/848. 
• Richard K. Guy (2004). Unsolved Problems in Number Theory, 3rd edition. Springer-Verlag. pp. Section B16. பன்னாட்டுத் தரப்புத்தக எண் 0-387-20860-7.
• Roger Heath-Brown]](1988). "Ternary quadratic forms and sums of three square-full numbers". Séminaire de Théorie des Nombres, Paris, 1986-7, 137–163, Boston:Birkhäuser.
• Heath-Brown, Roger(1990). "Sums of three square-full numbers". Number Theory, I (Budapest, 1987), 163–171, Colloq. Math. Soc. János Bolyai, no. 51.
• Ivić, Aleksandar (1985). The Riemann zeta-function. The theory of the Riemann zeta-function with applications. A Wiley-Interscience Publication. New York etc.: John Wiley & Sons. pp. 33–34, 407–413. பன்னாட்டுத் தரப்புத்தக எண் 0-471-80634-X. Zbl 0556.10026.
• McDaniel, Wayne L. (1982). "Representations of every integer as the difference of powerful numbers". Fibonacci Quarterly 20: 85–87. https://archive.org/details/sim_fibonacci-quarterly_1982-02_20_1/page/85. 
• Nitaj, Abderrahmane (1995). "On a conjecture of Erdős on 3-powerful numbers". Bulletin of the London Mathematical Society 27 (4): 317–318. doi:10.1112/blms/27.4.317. 

வெளி இணைப்புகள்

• The abc conjecture பரணிடப்பட்டது 2000-08-19 at the வந்தவழி இயந்திரம்