வகுஎண் சார்பு
எண்கோட்பாட்டில் வகுஎண் சார்பு (divisor function) என்பது ஒரு முழு எண்ணின் வகுஎண்களோடு தொடர்புடைய எண்கணிதச் சார்பு ஆகும் ரீமன் இசீட்டா சார்பியம் மீதான தொடர்புகள் உட்பட்ட பல முற்றொருமைகளில் இச்சார்பு பயன்படுத்தப்பட்டுள்ளது. [பல முக்கியமான சமானங்களையும் முற்றொருமைகளயும் கணிதவியலில் கண்டுபிடித்த இந்தியக் கணிதவியலாளர் இராமானுசன் வகுஎண் சார்பு குறித்தும் ஆய்வு செய்துள்ளார். அதுகுறித்த விவரங்கள் இராமானுசன் கூட்டு கட்டுரையில் தரப்பட்டுள்ளது.


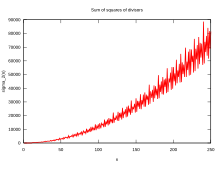
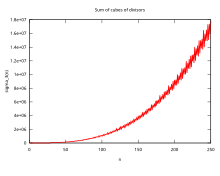
வரையறை தொகு
ஒரு சிக்கலெண் x இன் நேர் வகுஎண்கள் கூட்டுச் சார்பு (sum of positive divisors function) σx(n) என்பது, n இன் நேர் வகுஎண்களின் x ஆவது அடுக்குகளின் கூட்டுத்தொகையாக வரையறுக்கப்படுகிறது.
இச்சார்பினை கீழுள்ளவாறு எழுதலாம்:
- ( என்பது "n இன் வகுஎண் d" என்பதன் சுருக்கக் குறியீடு)
x = 0 எனும்போது கிடைக்கும் சார்பான σ0(n) என்பது வகுஎண்களின் எண்ணிக்கைச் சார்பு ஆகும். அதாவது σ0(n), n இன் வகுஎண்களின் எண்ணிக்கையைத் தருகிறது. d(n), ν(n), τ(n) (ஜெர்மானிய மொழியில் வகுஎண் என்பதற்கான சொல் Teiler) ஆகிய குறியீடுகளும் σ0(n) ஐக் குறிக்கப் பயன்படுத்தப்படுகின்றன.[1][2] (A000005).
x = 1 ஆக இருக்கும்போது இச்சார்பானது சிக்மா சார்பு (sigma function) அல்லது வகுஎண்களின் கூட்டுச் சார்பு (sum-of-divisors function) எனப்படுகிறது.[1][3] இக்குறியீட்டில் கீழொட்டு இல்லாமலும் எழுதலாம்:
- σ(n) = σ1(n) (A000203).
n இன் தகு வகுஎண் கூட்டுச் சார்பு -s(n):
இது n நீங்கலான அதன் பிற வகுஎண்களின் கூட்டுத்தொகையைக் குறிக்கும் சார்பு A001065).
- s(n) = σ1(n) − n
தகு வகுஎண் கூட்டுச் சார்பைத் தொடர்ந்து செயற்படுத்துவதன் மூலம் n இன் தகு வகுஎண்களின் கூட்டுத் தொடர்முறையைப் பெறலாம்.
எடுத்துக்காட்டு தொகு
12 இன் வகுஎண்களின் எண்ணிக்கைச் சார்பு σ0(12):
12 இன் வகுஎண்களின் வர்க்கங்களின் கூட்டுச் சார்பு σ1(12):
12 இன் தகு வகுஎண்களின் கூட்டுத்தொகை:
அட்டவணை தொகு
| n | வகுஎண்கள் | σ0(n) | σ1(n) | s(n) = σ1(n) − n | குறிப்பு |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | வர்க்கம் (கணிதம்): σ0(n) ஒற்றை; இரண்டின் அடுக்கு: s(n) = n − 1 |
| 2 | 1, 2 | 2 | 3 | 1 | பகா எண்: σ1(n) = 1 + n so s(n) = 1; இரண்டின் அடுக்கு: s(n) = n − 1 |
| 3 | 1, 3 | 2 | 4 | 1 | பகாஎண்: σ1(n) = 1 + n so s(n) = 1 |
| 4 | 1, 2, 4 | 3 | 7 | 3 | வர்க்க எண்: σ0(n) ஒற்றையெண்; இரண்டின் அடுக்கு: s(n) = n − 1 (almost-perfect) |
| 5 | 1, 5 | 2 | 6 | 1 | பகாஎண்: σ1(n) = 1 + n so s(n) = 1 |
| 6 | 1, 2, 3, 6 | 4 | 12 | 6 | முதல் நிறைவெண்: s(n) = n |
| 7 | 1, 7 | 2 | 8 | 1 | பகாஎண்: σ1(n) = 1 + n so s(n) = 1 |
| 8 | 1, 2, 4, 8 | 4 | 15 | 7 | இரண்டின் 2: s(n) = n − 1 |
| 9 | 1, 3, 9 | 3 | 13 | 4 | வர்க்க எண்: σ0(n) ஒற்றையெண் |
| 10 | 1, 2, 5, 10 | 4 | 18 | 8 | |
| 11 | 1, 11 | 2 | 12 | 1 | பகாஎண்: σ1(n) = 1 + n so s(n) = 1 |
| 12 | 1, 2, 3, 4, 6, 12 | 6 | 28 | 16 | முதல் மிகையெண் (கணிதம்): s(n) > n |
| 13 | 1, 13 | 2 | 14 | 1 | பகாஎண்: σ1(n) = 1 + n so s(n) = 1 |
| 14 | 1, 2, 7, 14 | 4 | 24 | 10 | |
| 15 | 1, 3, 5, 15 | 4 | 24 | 9 | |
| 16 | 1, 2, 4, 8, 16 | 5 | 31 | 15 | வர்க்க எண்: σ0(n) ஒற்றையெண்; இரண்டின் அடுக்கு: s(n) = n − 1 |
பண்புகள் தொகு
- n ஒரு வர்க்கமற்ற எண் எனில் அதன் ஒவ்வொரு வகுஎண் d , n இன் மற்றொரு வகுஎண் n/d இன் சோடியாக அமையும், இரட்டை எண்ணாக இருக்கும்.
- n ஒரு வர்க்க எண் எனில் அதன் ஒரு வகுஎண் ( ) n இன் வேறெந்தவொரு வகுஎண்ணுடனும் சோடியாக அமையாது, ஒற்றை எண்ணாக இருக்கும்.
- n வர்க்க எண்ணாகவோ அல்லது இரட்டை வர்க்க எண்ணாகவோ இருந்தால் மட்டுமே ஒற்றையெண்ணாக இருக்கும்.
p ஒரு பகாஎண் எனில்,
- ; σ(n) > n ( n > 2)
r = ω(n) என்பது n இன் வெவ்வேறான பகாக் காரணிகளின் எண்ணிக்கை, pi - i ஆவது பகாகாரணி, n ஐ வகுக்கக்கூடிய வகுஎண் pi இன் அதிகபட்ச அடுக்கு ai எனில்:
இம்முடிவு கீழ்வரும் வாய்பாடுக்குச் சமானமானது:
x = 0 எனில் d(n) :
n = 24 எனில்,
- இரு பகாக்காரணிகள் (p1 = 2; p2 = 3) உள்ளன. 24 = 23×31. எனவே a1 = 3; a2 = 1.
- ஐக் கீழுள்ளவாறு கணக்கிடலாம்:
- 24 இன் எட்டுக் காரணிகள்:
- 1, 2, 4, 8, 3, 6, 12, 24.
- s(n) = σ(n) − n.
- s(n), n இன் அனைத்து தகு வகுஎண்களின் கூட்டுத்தொகையைக் குறிக்கிறது. அதாவது n நீங்கலாக, n இன் மற்ற வகுஎண்களின் கூட்டுத்தொகையைத் தருகிறது. நிறைவெண்களை அடையாளங்காண இச்சார்பு பயன்படுகிறது.
- s(n) = n எனில், n ஒரு நிறைவெண்
- s(n) > n எனில், n ஒரு மிகையெண்
- s(n) < n எனில், n ஒரு குறைவெண்
n இரண்டின் அடுக்காக இருக்குமானால் ( ):
- இதனால் n ஒரு கிட்டத்தட்ட நிறைவெண்ணாக இருக்கும்.
தொடர்களில் தொகு
வகுஎண் சார்பைக் கொண்டுள்ள இரு டிரிழ்ச்லெட் தொடர்கள்:
இதிலிருந்து d(n) = σ0(n):
வகுஎண் சார்பைக் கொண்டுள்ள லாம்பெர்ட் தொடர்:
- (குறிப்பிலா சிக்கலெண் |q| ≤ 1 and a)
குறிப்புகள் தொகு
- ↑ 1.0 1.1 (Long 1972, ப. 46)
- ↑ (Pettofrezzo & Byrkit 1970, ப. 63)
- ↑ (Pettofrezzo & Byrkit 1970, ப. 58)
மேற்கோள்கள் தொகு
- Akbary, Amir; Friggstad, Zachary (2009), "Superabundant numbers and the Riemann hypothesis" (PDF), American Mathematical Monthly, 116 (3): 273–275, doi:10.4169/193009709X470128, archived from the original (PDF) on 2014-04-11, பார்க்கப்பட்ட நாள் 2016-08-03.
- Eric Bach|Bach, Eric; Jeffrey Shallit|Shallit, Jeffrey, Algorithmic Number Theory, volume 1, 1996, MIT Press. பன்னாட்டுத் தரப்புத்தக எண் 0-262-02405-5, see page 234 in section 8.8.
- Caveney, Geoffrey; Nicolas, Jean-Louis; Sondow, Jonathan (2011), "Robin's theorem, primes, and a new elementary reformulation of the Riemann Hypothesis" (PDF), INTEGERS: the Electronic Journal of Combinatorial Number Theory, 11: A33
- Choie, YoungJu; Lichiardopol, Nicolas; Moree, Pieter; Solé, Patrick (2007), "On Robin's criterion for the Riemann hypothesis", Journal de théorie des nombres de Bordeaux, 19 (2): 357–372, arXiv:math.NT/0604314, doi:10.5802/jtnb.591, ISSN 1246-7405, MR 2394891, Zbl 1163.11059
- Grönwall, Thomas Hakon (1913), "Some asymptotic expressions in the theory of numbers", Transactions of the American Mathematical Society, 14: 113–122, doi:10.1090/S0002-9947-1913-1500940-6
- Ivić, Aleksandar (1985), The Riemann zeta-function. The theory of the Riemann zeta-function with applications, A Wiley-Interscience Publication, New York etc.: John Wiley & Sons, pp. 385–440, ISBN 0-471-80634-X, Zbl 0556.10026
- Lagarias, Jeffrey C. (2002), "An elementary problem equivalent to the Riemann hypothesis", The American Mathematical Monthly, 109 (6): 534–543, doi:10.2307/2695443, ISSN 0002-9890, JSTOR 2695443, MR 1908008
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
- Ramanujan, Srinivasa (1997), "Highly composite numbers, annotated by Jean-Louis Nicolas and Guy Robin", The Ramanujan Journal, 1 (2): 119–153, doi:10.1023/A:1009764017495, ISSN 1382-4090, MR 1606180
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77081766
- Robin, Guy (1984), "Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann", Journal de Mathématiques Pures et Appliquées, Neuvième Série, 63 (2): 187–213, ISSN 0021-7824, MR 0774171
- Williams, Kenneth S. (2011), Number theory in the spirit of Liouville, London Mathematical Society Student Texts, vol. 76, Cambridge: கேம்பிறிட்ஜ் பல்கலைக்கழகப் பதிப்பகம், ISBN 978-0-521-17562-3, Zbl 1227.11002
- Weisstein, Eric W., "Divisor Function", MathWorld.
- Weisstein, Eric W., "Robin's Theorem", MathWorld.
- Elementary Evaluation of Certain Convolution Sums Involving Divisor Functions PDF of a paper by Huard, Ou, Spearman, and Williams. Contains elementary (i.e. not relying on the theory of modular forms) proofs of divisor sum convolutions, formulas for the number of ways of representing a number as a sum of triangular numbers, and related results.