விண்மீன் கோட்டுரு
கோட்டுருவியலில் விண்மீன் அல்லது விண்மீன் கோட்டுரு (star) Sk என்பது முழு இருகூறு கோட்டுருவாகும். இக்கோட்டுரு ஒரு உள்முனையும் k இலைகளும் கொண்ட மரமாக (K1,k) இருக்கும். k ≤ 1 எனில் இம்மரத்தில் உள்முனை இருக்காது, k + 1 இலைகள் இருக்கும்).
| விண்மீன் | |
|---|---|
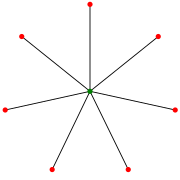 விண்மீன் S7. (சிலர் இதனை S8 என்றும் குறிப்பதுண்டு.) | |
| முனைகள் | k+1 |
| விளிம்பு | k |
| விட்டம் | (2, k) இன் சிறுமவளவு |
| சுற்றளவு | ∞ |
| நிற எண் | (2, k + 1) இன் சிறுமவளவு |
| நிறச் சுட்டெண் | k |
| இயல்புகள் | விளிம்புக்-கடப்பு மரம் அலகு தொலைவு இருகூறானது |
| Notation | Sk |
மாறாக, சில நூலாசிரியர்கள் விண்மீனை (Sk) அதிகபட்சம் 2 அலகு விட்டமும் k வரிசையும் கொண்ட மரமாக வரையறுக்கின்றனர். இந்த வகையில் k > 2 எனில் அந்த விண்மீனில் k − 1 இலைகள் இருக்கும்
ஒன்றுக்கும் அதிகமான படிகொண்ட அதிகபட்ச முனைகள் ஒன்று மட்டுமேயுள்ள இணைப்புள்ள கோட்டுருக்களாகவும் விண்மீன் கோட்டுருக்களை வரையறுக்கலாம்.
கவ்வி
தொகுமூன்று படியுடைய விண்மீன் கவ்வியென (claw) அழைக்கப்படுகிறது.
கவ்வியற்றக் கோட்டுருக்களின் வரையறையில் கவ்விகள் குறிப்பிடத்தக்கவை. கவ்வியற்ற கோட்டுருக்களின் எந்தவொரு தூண்டப்பட்ட உட்கோட்டுருவும் கவ்வியாக இருக்காது.[1][2]
பயன்பாடுகள்
தொகுபல கோட்டுரு பண்புகள் விண்மீன்களைக் கொண்டு வரையறுக்கப்பட்டுள்ளன:
- ஒரு கோட்டுருவைக் காடுகளாகப் பிரிக்கும்போது அக்காடுகளிலுள்ள ஒவ்வொரு மரமும் ஒரு விண்மீனாக இருக்கவேண்டும் என்ற கட்டுப்பாட்டுக்குட்பட்டு பிரிக்கப்படக்கூடிய காடுகளின் என்ணிக்கையின் சிறுமமதிப்பு விண்மீன் எண்ணிக்கை (Star arboricity) எனப்படும்.[3]
- ஒரு கோட்டுருவின் "விண்மீன் நிற எண்" என்பது "ஒவ்வொரு இரண்டு நிறத் தொகுதிகள் இணைந்து உருவாக்கும் உட்கோட்டுருக்களின் இணைப்புள்ள கூறுகள் அனைத்தும் விண்மீன்களாக இருக்க வேண்டும்" என்பதற்குட்பட்டு அக்கோட்டுருவின் முனைகளை நிறந்தீட்டத் தேவைப்படும் நிறங்களின் எண்ணிக்கையின் சிறுமவளவு ஆகும்.[4]
- கிளை அகலம் 1 உடைய கோட்டுருக்களின் ஒவ்வொரு இணைப்புள்ள கூறுகளும் ஒரு விண்மீனாக இருக்கும்.[5]
இதர பயன்பாடுகள்
தொகு- ஒரு கவ்வியின் முனைகளுக்கு இடைப்பட்ட தொலைவுகளின் கணம், சமவளவை உருமாற்றத்தால் எப்பரிமாண யூக்ளிடிய வெளிக்குள்ளும் உட்பொதிய முடியாத ஒரு முடிவுறு மெட்ரிக் வெளிக்கு எடுத்துக்காட்டாக அமைகிறது.[6]
- விண்மீன் கோட்டுருவை மாதிரியாகக் கொண்ட கணினி வலையமைப்பான விண்மீன் வலையமைப்பு, விரவல் கணினி செய்முறையில் முக்கியமான ஒன்றாகும்.
மேற்கோள்கள்
தொகு- ↑ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics, 164 (1–3): 87–147, எண்ணிம ஆவணச் சுட்டி:10.1016/S0012-365X(96)00045-3, MR 1432221.
- ↑ Chudnovsky, Maria; Seymour, Paul (2005), "The structure of claw-free graphs", Surveys in combinatorics 2005 (PDF), London Math. Soc. Lecture Note Ser., vol. 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR 2187738.
- ↑ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), "Star arboricity of graphs", Discrete Math., 149: 93–98, எண்ணிம ஆவணச் சுட்டி:10.1016/0012-365X(94)00313-8
- ↑ Fertin, Guillaume; Raspaud, André; Reed, Bruce (2004), "Star coloring of graphs", Journal of Graph Theory, 47 (3): 163–182, எண்ணிம ஆவணச் சுட்டி:10.1002/jgt.20029.
- ↑ Robertson, Neil; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory, 52 (2): 153–190, எண்ணிம ஆவணச் சுட்டி:10.1016/0095-8956(91)90061-N.
- ↑ Linial, Nathan (2002), "Finite metric spaces–combinatorics, geometry and algorithms", Proc. International Congress of Mathematicians, Beijing, vol. 3, pp. 573–586, arXiv:math/0304466, Bibcode:2003math......4466L