ஈர்ப்பு விசை
ஈர்ப்பு விசை அல்லது பொருள் ஈர்ப்பு விசை அல்லது புவி ஈர்ப்பு விசை (gravitational force) என்பது இயற்கையாக பொருட்கள் ஒன்றை ஒன்று கவர்ந்து கொள்ளும் விசை, அவற்றின் திணிவுகளின் பெருக்கத்துக்கு நேர்விகிதத்தில் இருப்பது ஆகும். ஈர்ப்பு விசை என்பது பொருட்களை கைவிடும் பொழுது அவை கீழே விழுவதற்கும் மற்றும் அவைகளுக்கு எடையை கொடுப்பதுவுமே ஆகும். அண்டத்தில் உள்ள ஏதேனும் இரு பொருள்களுக்கு இடையே செயல்படுவது ஈர்ப்பு விசை ஆகும். இவ்விசையானது பொருள்களின் திணிவுகளைச் சார்ந்த கவர்ச்சி விசையாகும். அடிப்படை விசைகளில், பொருள் ஈர்ப்பு விசையே மிகவும் வலிமை குன்றிய விசையாகும். ஆனால் அண்டத்தில் நெடுந்தொலைவிற்குச் செயல்படக் கூடியது. இது 'ஈர்ப்பியல் விசை' எனவும் வழங்கப்படும். ஈர்ப்பு விசை பிரிந்திருக்கும் பொருட்களை ஒன்று சேர்ப்பதற்கும், ஒன்று சேர்ந்த பொருட்கள் அப்படியே இருப்பதற்கும் உதவுகிறது. இதனால் பூமி, சூரியன், மற்றும் பிரபஞ்சத்தில் உள்ள பரவலான பொருட்கள் அப்படியே இருப்பதற்குப் பங்களிக்கிறது.
பூமி மற்றும் ஏனைய கோள்களை அதன் சுற்றுப்பாதையில் சுற்ற வைப்பதற்கும்; சந்திரன் பூமியை சுற்றி வருவதற்கும்; அலைகள் உருவாவதற்கும்; திரவ போக்கு அதன் அடர்த்தி மாறல் விகிதம் மற்றும் புவியீர்ப்பை பொறுத்து செல்வதற்கும்; உருவாகும் நட்சத்திரங்கள் மற்றும் கோள்களின் உள்ளே அதிக வெப்பம் உருவாகுவதற்கும்; மற்றும் பூமியில் காணப்படும் பல்வேறு நிகழ்வுகள் இடம் பெறுவதற்கும் காரணியாக ஈர்ப்பு விசை உள்ளது.
ஈர்ப்பு விசை, மின்காந்த விசை, வலுவான அணுக்கரு விசை, வலு குன்றிய அணுக்கரு விசை ஆகியன இயற்கையின் நான்கு அடிப்படை விசைகள் ஆகும். நவீன இயற்பியல் ஈர்ப்பு விசையை, ஐன்ஸ்டீனின் பொது சார்பியல் கோட்பாடு மூலமாக அனைத்து அசைவற்ற பொருட்களின் இயக்கத்தை விளக்குகிறது. நியூட்டனின் எளிய பிரபஞ்ச ஈர்ப்பு விதி மிக அதிக இடங்களில் துல்லியமான தோராய மதிப்பை வழங்குகிறது.
ஈர்ப்பு கோட்பாடு வரலாறு
தொகு| மரபார்ந்த விசையியல் | ||||||||
வரலாறு · காலக்கோடு
| ||||||||
அறிவியல் புரட்சி
தொகுஈர்ப்பு கோட்பாட்டின் தற்கால வேலை 16 ஆம் நூற்றாண்டின் இறுதியில் மற்றும் 17 ஆம் நூற்றாண்டின் ஆரம்பத்தில் கலிலியோ கலிலியால் தொடங்கப்பட்டது. அவரது புகழ்பெற்ற (எனினும் இது உறுதிப்படாத [1]) சோதனையான பீசா கோபுரத்தில் இருந்து பந்துகளை விட்டது, பின்னர் சாய்வுகளில் பந்துகளை கவனமாக அளவிட்டதன் மூலமாக கலிலியோ ஈர்ப்பு விசை அனைத்து பொருட்களையும் ஒரே வேகத்தில் துரிதப்படுத்துகிறது என்று காட்டினார். இது அரிஸ்டாடிலின் கொள்கையான கனமான பொருட்கள் அதிகமான வேக வளர்ச்சி கொண்டவை என்பதை மாற்றியது. [2] இலகுவான பொருட்கள் காற்றின் எதிர்ப்பினால் வளிமண்டலத்தில் மிகவும் மெதுவாக விழும் என்று கலிலியோ சரியாக சொன்னது ஒப்புக்கொள்ளப்பட்டுள்ளது. கலிலியோவின் வேலை நியூட்டனின் ஈர்ப்பு விசை கோட்பாடு உருவாக உதவியது.
நியூட்டனின் ஈர்ப்பு கோட்பாடு
தொகு
1687 ஆம் ஆண்டு, ஆங்கில கணித மேதை சர் ஐசக் நியூட்டன் பிரின்சிப்பியா என்னும் அறிவியல் இதழில் பிரபஞ்ச ஈர்ப்பு நேர்மாறான சதுர விதியை (Inverse Square Law) வெளியிட்டார். அவரது சொந்த வார்த்தைகளில், "கோள்கள் அவற்றின் சுற்றுப்பாதையில் சுற்றி வரச்செய்யும் விசை அவற்றின் ஆரத்திற்கு எதிர்மறையாக இருக்கும்" என்பதைக் கண்டறிந்தார். மேலும் அவர் இந்தக் கருத்தை சந்திரனுக்கும் பூமிக்கும் பயன்படுத்தினார். அவைகள் ஏறக்குறைய ஒத்துப்போவதை அறிந்தார்.
யுரேனஸ் நகர்வுகளை அடிப்படையாக கொண்டு நெப்டியூன் இருப்பதைக் கண்டறிய பயன்படுத்தப்படும் போது நியூட்டனின் கோட்பாடு, அதன் மிகப் பெரிய வெற்றியைக் கண்டது. இது மற்ற கிரகங்கள் நடவடிக்கைகளின் மூலமாக அறிய முடியாது. ஜான் கோச் ஆடம்ஸ் (John Couch Adams) மற்றும் அற்பெயின் லு வெரியர் (Urbain Le Verrier) ஆகிய இருவரின் கணக்கீடுகளை கொண்டு கிரகத்தின் பொது நிலையைக் கணித்து, லு வெரியரின் கணக்கின்படி, ஜோஹ்ன் கோட்ஃபிரெய்ட் காலி(Johann Gottfried Galle) நெப்ட்டியுனை கண்டுபிடித்தார்.
புதனின் சுற்றுப்பாதையில் உள்ள ஒரு முரண்பாடு நியூட்டனின் கோட்பாட்டில் உள்ள குறைபாடுகளைச் சுட்டிக் காட்டியது. 19 ஆம் நூற்றாண்டின் இறுதியில், அதன் சுற்றுப்பாதையில் இருந்த சிறிய குழப்பம் நியூட்டனின் கோட்பாடு கீழ் முற்றிலும் கணக்கில் கொள்ள முடியாது என்று அறியப்பட்டது, ஆனால் மற்றொரு கிரகத்தின் (மெர்குரியை விட சூரியனை நெருக்கமாக சுற்றிவரும் ஒரு கிரகம்) அனைத்து தேடல்களும் பலனற்றதாயிற்று. 1915 இல் இந்த பிரச்சினை ஆல்பர்ட் ஐன்ஸ்டீனின் புதிய பொது சார்பியல் கோட்பாடு மெர்குரியின் சுற்றுப்பாதையில் உள்ள சிறிய முரண்பாடுகளை கணக்கில் கொண்டு தீர்க்கப்பட்டது.
நியூட்டனின் கோட்பாடு அகற்றப்பட்டுவிட்டது என்றாலும்,தற்கால சார்பின்மை ஈர்ப்பு கணக்குகள் பொது சார்பியல் கோட்பாடை விட எளிமையான நியூட்டனின் கோட்பாட்டை பயன்படுத்தி செய்யப்படும், மற்றும் போதுமான அளவு சிறிய எடைகள், வேகம் மற்றும் ஆற்றல் சம்பந்தப்பட்ட பெரும்பாலான பயன்பாடுகளுக்கு போதுமான அளவு துல்லியமான முடிவுகளை கொடுக்கிறது. நியூட்டனின் ஈர்ப்பியல் விதிப்படி, ஈர்ப்பு விசையானது, திணிவுகளின் பெருக்கற்பலனுக்கு நேர்த்தகவிலும், அவற்றிற்கிடையேயுள்ள தொலைவின் இருமடிக்கு எதிர்த்தகவிலும் இருக்கும். அதாவது, m1 ,m2 என்பன இரு பொருள்களின் நிறை எனவும் r என்பது அவற்றிற்கு இடைப்பட்ட தொலைவு எனவும் கொண்டால், இவ்விரு பொருள்களுக்கு இடையேயான ஈர்ப்பு விசை,
G என்பது ஈர்ப்பியல் மாறிலி. இதன் மதிப்பு 6.67 x 10−11 N m2 kg−2. SI அலகு முறைப்படி,நிறையின் அலகு கிலோகிராம்(kg) எனவும் தூரத்தின் அலகு மீட்டர்(m) எனவும் கொடுக்கப் பெற்றால் விசையின் அலகு நியூட்டன்(N) ஆகும்.
சமானத் தத்துவம்
தொகுகலிலியோ, லோராண்டு எட்வோஸ் (Loránd Eötvös), மற்றும் ஐன்ஸ்டீன் உட்பட ஆராய்ச்சியாளர்களால் அடுத்தடுத்து வெளிக்கொணரப்பட்ட சமநிலை கோட்பாடு, அனைத்து பொருட்களும் ஒரே மாதிரி விழும் என்று கருத்து தெரிவித்துள்ளது. பலவீனமான சமநிலை கோட்பாடு சோதிக்க எளிய வழி ஒரு வெற்றிடத்தில் வெவ்வேறு எடை அல்லது கலவை கொண்ட இரண்டு பொருட்களை விட்டு, அவை ஒரே நேரத்தில் தரையில் விழுந்ததா என்று பார்ப்பதாகும். இந்த சோதனைகள் உராய்வு (காற்று எதிர்ப்பு உட்பட) புறக்கணிக்கத்தக்கதாக இருக்கும்போது அனைத்து பொருட்களும் அதே விகிதத்தில் விழுகிறது என்று நிரூபிக்கின்றது. மேலும் நவீன சோதனைகள் Eötvös கண்டுபிடித்த ஒரு வகை ஒரு திருகு(torsion) சமநிலையை பயன்படுத்தியது. செயற்கைக்கோள் சோதனைகள், எடுத்துக்காட்டாக ஸ்டெப்-செயற்கைகோள், விண்வெளியில் துல்லியமாக பரிசோதனை செய்ய திட்டமிடப்பட்டுள்ளது.
சமநிலை கோட்பாடு உருவாக்கங்கள் பின்வருமாறு:
- பலவீனமான சமநிலை கோட்பாடு: ஒரு ஈர்ப்பு புலத்தில் ஒரு புள்ளி நிறையின் போக்கு, அதன் ஆரம்ப நிலை மற்றும் வேகத்தை மட்டுமே சார்ந்துள்ளது, மற்றும் அதன் அமைப்பை பொறுத்து அல்ல .
- ஐன்ஸ்டினியன் சமநிலை கோட்பாடு:. தடையின்றி விழும் ஆய்வகத்தில் எந்த ஒரு ஈர்ப்பு அல்லாத சோதனையின் முடிவு, ஆய்வகத்தின் காலம், இடம் மற்றும் வேகத்தை சார்ந்திருக்காது.
- வலுவான சமநிலை கோட்பாட்டுக்கு மேலே உள்ள இரண்டும் தேவை.
பொது சார்பியல்
தொகு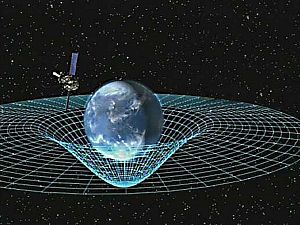
பொது சார்பியலில், ஈர்ப்பின் விளைவுகள் விசைக்கு பதிலாக காலவெளி வளைவு மூலமாக நடக்கிறது. பொது சார்பியலின் ஆரம்ப புள்ளி நிலைமை இயக்கத்தையும் தடையின்றி விழுதலையும் சமன்படுத்துதலாகும், மற்றும் தடையின்றி விழும் நிலைமை பொருட்கள், தரையில் துரிதப்படுத்தும் பார்வையாளர்களின் ஒப்புமையில் வேகம் அதிகரித்தலையும் சமநிலை கோட்பாடு விவரிக்கின்றது. நியூட்டனின் இயற்பியலில், பொருட்களை குறைந்த பட்சம் ஒரு விசை மூலம் இயக்கபட்டாலொழிய அத்தகைய முடுக்கம் ஏற்படாது.
ஐன்ஸ்டீன், பொருட்கள் காலவெளியை வளைக்கின்றன என்பதையும், தடையற்று விழும் பொருட்கள், வளைந்த காலவெளி இடத்தில், நேரான பாதைகள் வழியாக செல்கின்றன என்றும் கூறினார். இந்த நேர் பாதைகள் புவியின் மேற்பரப்பிற்குரியவைகள் என்று அழைக்கப்படுகின்றன. நியூட்டனின் முதல் இயக்க விதி போல், ஐன்ஸ்டீனின் கோட்பாடு ஒரு பொருளின் மீது விசை பயன்படுத்தப்படும் போது, அது ஒரு புவிப்பரப்பில் இருந்து விலகுகிறது என்று கூறுகிறது. உதாரணமாக, தரையில் உறைநிலையற்ற நிலையில் நிற்கும்போது நாம் புவிமேற்பரப்புகளை பின்பற்றுவதில்லை. ஏனெனில் பூமியின் இயந்திர எதிர்ப்பு நம்மேல், விசையை செலுத்துகிறது. காலவெளியில் புவிமேற்பரப்புகளோடு சேர்ந்து நகருவதை, அசைவற்றதாக கருதுவதை இது விளக்குகிறது.
ஐன்ஸ்டீன் பெருட்கள் இருப்பதையும் காலவெளி வளைவுகளையும் தொடர்புபடுத்தும் போது, சார்பியலில் புல சமன்பாடுகளை கண்டறிந்தார்.அதனால் அந்த சமன்பாடுகளுக்கு அவர் பெயர் வந்தது. ஐன்ஸ்டீனின் புல சமன்பாடுகள் ஒரே நேரத்தில் 10, நேர்கோடற்ற, வகைக்கெழு சமன்பாடுகளின் தொகுப்பாகும். புல சமன்பாடுகளின் தீர்வுகள், காலவெளியின் மீற்றரிழுவம் (metric tensor) கூறுகளாகும். ஒரு மீற்றரிழுவம், காலவெளியின் வடிவவியலை விளக்குகிறது. ஒரு காலவெளியின் கோளமேற்பரப்பிற்குரியவைகளின் பாதைகள், மீற்றரிழுவம் மூலம் கணக்கிடப்படுகிறது.
ஐன்ஸ்டீனின் புல சமன்பாடுகளின் குறிப்பிடத்தக்க தீர்வுகள் பின்வருமாறு:
- Schwarzschild தீர்வு என்பது ஒரு கோள வடிவில் சமச்சீர் சுழலும் மின்னூட்டமற்ற பெரும் பொருள் சுற்றியுள்ள காலவெளியை விவரிப்பதாகும். சிறிய அளவு பொருட்களை, இந்த தீர்வு மைய ஒருமைத்தன்மையுடன் ஒரு கரும்புள்ளியை உருவாக்கியது. Schwarzschild ஆரத்தை விட அதிகமான தூரத்தில் இருக்கும் முடுக்கம் நியூட்டனின் ஈர்ப்பு விசை கோட்பாட்டின் மூலம் கணிக்கப்பட்டதற்கு சமமாக உள்ளது.
- Reissner-Nordström தீர்வில் மத்திய பொருளுக்கு மின்னூட்டம் உண்டு.
- கெர் தீர்வு: சுழலும் பொருட்களுக்கான விளக்கமாகும். இந்த தீர்வு பல நிகழ்வு எல்லைகளில் கறுப்பு ஓட்டைகளை உற்பத்தி செய்கிறது.
- கெர்-நேவ்மன் தீர்வு: மின்னூட்டம் பெற்ற, சுழலும் பொருட்களுக்கு ஆகும். இந்த தீர்வு பல நிகழ்வு எல்லைகளை கறுப்பு ஓட்டைகள் உற்பத்தி செய்கிறது.
- பிரபஞ்சத்தின் விரிவாக்கத்தை அண்டவியல் ஃப்ரைடுமேன்-லேமைட்ரீ-ராபர்ட்சன், வாக்கரின் தீர்வு
பொது சார்பியல் சோதனைகளை கணித்துள்ளது. கள் பின்வரும் அடங்கும்:
- பொது சார்பியல் புதனின் முரண்பாடான சிறும வீச்சுக்கு காரணம் கூறுகிறது.
- நேரம் மெதுவாக இயங்கும் கணிப்பை பவுண்ட்-ரெபக்கா சோதனை, ஹபிலே-கீட்டிங் சோதனை, மற்றும் ஜி.பி. எஸ் மூலம் உறுதி செய்யப்பட்டுள்ளது.
- ஒளியின் விலகலை முதன்முதலில் மே 29, 1919 ஆம் ஆண்டு சூரிய கிரகணத்தின் போது ஆர்தர் ஸ்டான்லி எட்டிங்க்டன் தனது அவதானிப்புகள் மூலம் உறுதி செய்தார். எட்டிங்க்டன் பொது சார்பியல் கணிப்புகளும், நியூட்டனின் துகள் கொள்கை கணிப்புகளும் இணங்க, இருமுறை ஸ்டார்லைட் விலக்கங்களை அளவிட்டார். இருப்பினும், அவரது முடிவுகைளின் விளக்கம் பின்னர் மறுக்கப்பட்டது. சூரியனின் பின்னால் செல்லும் குவாசார்கள் செலுத்து ரேடியோ interferometric அளவீடுகளை பயன்படுத்தி சமீபத்திய பரிசோதனைகள் மூலம் இன்னும் துல்லியமாக, பொது சார்பியல் கோட்பாடு மூலம் கணித்து அளவிற்கு ஒளி விலகல் உறுதி செய்யப்பட்டுள்ளது. மேலும் ஈர்ப்பு லென்ஸ் பார்க்க.
- ஒரு பெரிய பொருள் நெருக்கமாக கடந்து செல்லும் போது ஒளியின் நேரம் தாமதமாவதை கிரகங்களுக்கு இடையிலான விண்வெளி சமிக்ஞைகளை மூலம் 1964 இல் இர்வின் முதலாம் ஷாபிரோ அடையாளம் கண்டார்.
- ஈர்ப்பு கதிர்வீச்சு மறைமுகமாக, பைனரி பல்சர்கள் ஆய்வுகள் மூலம் உறுதி செய்யப்பட்டுள்ளது.
- 1922 ஆம் ஆண்டில் அலெக்ஸாண்டர் ஃப்ரைடுமேன் ஐன்ஸ்டீனின் சமன்பாடுகளை நிலையற்ற தீர்வுகளை (அண்டவியல் மாறிலி முன்னிலையில் கூட) கொண்டுள்ளது என்று கண்டறியப்பட்டது. 1927 ல் ஜார்ஜ் லேமைட்ரீ அண்டவியல் மாறிலி முன்னிலையில் ஐன்ஸ்டீனின் சமன்பாடுகள், நிலையான தீர்வுகள் நிலையற்றது என்று காட்டினார், மற்றும் ஐன்ஸ்டீன் கூறிய நிலையான பிரபஞ்சம் இருக்க முடியாது என்று கூறினார். பின்னர், 1931 ஆம் ஆண்டு, ஐன்ஸ்டீன் ஃப்ரைடுமேன் மற்றும் லேமைட்ரீ முடிவுகளுக்கு உடன்பட்டார். இதனால் பொது சார்பியல் பேரண்டம் நிலையற்றதென்றும் ஒன்று அது விரியும் அல்லது சுருங்கும் என்று கணிக்கப்பட்டுள்ளது. 1929 ல் எட்வின் ஹப்பிள் பிரபஞ்சத்தின் விரிவாக்கத்தை உறுதி செய்தார்.
- சட்ட இழுப்பு கோட்பாட்டின் கணிப்பு சமீபத்தில் ஈர்ப்பு ஆய்வு B முடிவுக்கு இசைவானதாக இருந்தது.
- பொது சார்பியல் அதிக எடை கொண்ட பொருட்களில் இருந்து ஒளி பயணிக்கும் போது அதன் ஆற்றல் இழக்க வேண்டும் கணித்துள்ளது. கோபன்ஹேகன் பல்கலைக்கழகத்தில் நீல்ஸ் போர் கல்லூரி Radek Wojtak குழு 8000 க்லசட்டர் மண்டலங்களில் இருந்து எடுக்கப்பட்ட தகவல்கள் மூலம் க்ளுச்டேர்களின் மையத்தில் இருந்து வரும் ஒளி அலைகள் விளிம்பில் இருந்து வருவதை காட்டிலும் சிவப்பு பெயர்ச்சி அடைந்துள்ளதை, ஈர்ப்பின் மூலமாக சக்தி குறைந்துள்ளதை காட்டுகிறது.
ஈர்ப்பு மற்றும் குவாண்டம் மெக்கானிக்ஸ்
தொகுபொது சார்பியல் கண்டுபிடித்து பல தசாப்தங்களுக்கு பின்நறும் பொது சார்பியலும் குவாண்டம் மெக்கானிக்ஸ் இணக்கமற்றது என்று உணரப்பட்டது. குவாண்டம் புல கொள்கையின் கட்டமைப்பிற்குள் மற்ற அடிப்படை விசைகள் போல் இது ஈர்ப்பு கவர்ச்சி விசையில் மின்காந்த விசையில் போட்டான்கள் பரிமாற்றம் நடப்பது போலவே, இங்கு க்ராவிட்டன்ஸ் பரிமாற்றம் காரணமாக விசை உருவாகிறது என்று விவரிக்க முடியும். இது கிளாசிக்கல் வரம்பில் பொது சார்பியலை மீண்டும் உருவாக்கியது. எனினும், இந்த அணுகுமுறையை குறுகிய நீளங்களில் ப்ளாங்க் நீளத்தில் அணுகமுடியாது. குவாண்டம் ஈர்ப்பின் (அல்லது குவாண்டம் மெக்கானிக்சுக்கு ஒரு புதிய அணுகுமுறை) முழுமையான கோட்பாடு தேவையாகும்.
குறிப்பிட்டவைகள்
தொகுபூமியின் ஈர்ப்பு
தொகுஒவ்வொரு கிரக அமைப்பும் (பூமி உட்பட) அதன் சொந்த ஈர்ப்பு புலத்தால் சூழப்பட்டுள்ளது. அது அனைத்து பொருட்களின் மீது ஒரு கவரும் விசையை செலுத்துகிறது . ஒரு கோள வடிவில் சமச்சீர் கிரகத்தில் அனுமானித்து, எந்த ஒரு இடத்திலும் அதனின் புலத்தின் சக்தி கோள்களின் எடைக்கு நேர்விகிதத்திலும் மற்றும் உடல் மையத்தில் இருந்து அந்த இடத்தின் தூரம் சதுர எதிர் விகிதாசாரத்திலும் இருக்கும்.
ஈர்ப்புமண்டலத்தை வலிமை அதன் தாக்கத்தின் கீழ் இருக்கும் பொருள்களின் முடுக்கத்திற்கு சமமாகவும் பூமியின் மேற்பரப்பில், அதன் மதிப்பு, கிட்டத்தட்ட நிலையான சராசரி கீழே g என வெளிப்படுத்தப்படுகிறது.
g = 9,81 M / s 2 = 32.2 அடி / s 2
காற்றின் எதிர்ப்பை புறக்கணித்து விட்டோமானால், ஒரு பொருள் பூமியின் மேற்பரப்பின் அருகில் தடையின்றி விழும் பொழுது, அதன் வேகம் நொடிக்கு 9.81 M / s (32.2 அடி / கள் அல்லது 22 மைல்) அதிகரிக்கிறது, என்று பொருள். அதாவது, ஓய்வு நிலையில் இருந்து தொடங்கும் ஒரு பொருள் ஒரு நொடியில் 9.81M / s (32.2 அடி / s) என்ற வேகத்தை அடையும்,இரண்டு விநாடிகள் கழித்து 19,62 M / s (64.4 அடி / கள்) என்ற வேகத்தை அடையும், மற்றும் ஒவ்வொரு 9.81M / s(32,2 அடி / s ) சேர்த்து அதன் வேகம் கிடைக்கும். மேலும், காற்று எதிருப்பு இல்லாத போது ஒரே உயரத்தில் இருந்து விழும் அனைத்து பொருட்களும், ஒரே நேரத்தில் தரையில் விழும்.

நியூட்டனின் 3 ஆம் விதிப்படி, பூமி தன் மீது விழும் பொருளின் மேல் செலுத்தும் அதே அளவு விசையை தானும் ஆனால் அதன் திசை அது செலுத்தும் திசைக்கு எதிர் திசையில் இருக்கும். அந்த பொருள் பூமி மீது மோதும் வரை பூமி பொருளை நோக்கி முடுக்கப்படுகிறது என்று பொருள். பூமியின் நிறை அதிகம் என்பதால்,இந்த எதிர் விசை மூலம் பூமிக்கு அளித்த முடுக்கம் பொருளுடன் ஒப்பிடுகையில் புறக்கணிக்கத்தக்கதாகும். அந்த பொருள் பூமியின் மீது மோதிய பிறகு திரும்பி எழவில்லையெனில் இரண்டும் தங்களுக்குள் விளக்கு விசையை செலுத்தியுள்ளன. அது பொருளின் ஈர்ப்பு விசையை சமன்படுத்தி மேலும் முடுக்கத்தை நிறுத்துகிறது.
பூமியின் மேற்பரப்பில் அருகே விழும் பொருட்களின் சமன்பாடுகள்
தொகு
தொடர்ச்சியான ஈர்ப்பின் கீழ், பிரபஞ்ச ஈர்ப்பு நியூட்டனின் விதி எளிமையாக்கும் வகையில் F = mg, m என்பது பெருளின் நிறை மற்றும் g என்பது 9 .81 M / s 2 என்ற சராசரி அளவு கொண்ட ஒரு நிலையான வெக்டார். ஈர்ப்பின் முடுக்கம் இந்த g க்கு சமமாக இருக்கும். ஈர்ப்பின் கீழ் ஆரம்பத்தில் நிலையான நிலையில் இருந்து தடையின்றி விழும் பொருளின் கடந்துவிட்ட தூரம்அதன் நேரத்துக்கு சதுர நேர்விகிதத்தில் ஒரு குறைகிறது. வலப்பக்கம் உள்ள படம் அரை நொடி கால வெளியில் நொடிக்கு 20 ப்ளாஷ் விகிதத்தில் stroboscopic ப்ளாஷ் கொண்டு கைப்பற்றப்பட்டது 20 நொடியில் ஒரு பங்கு நேரத்தில் பந்து ஒரு அலகு தூரத்தை கடந்துள்ளது; (இங்கு ஒரு அலகு என்பது 12 மிமீ); இரண்டு பங்கு நேரத்தில் 4 அலகு தூரத்தையும்; 3 பங்கு நேரத்தில் 9 அலகு தூரத்தையும் கடந்தது.
ஒரே சீரான ஈர்ப்பு என்ற ஊகத்தின் கீழ் h என்ற உயரத்தில் உள்ள ஒரு பொருளின் நிறை ஆற்றல் E= mgh (அல்லது E = Wh, W என்பது எடை.) இந்த சமன்பாடு பூமியின் மேற்பரப்பில் இருந்து சிறிய தூரங்களில் h மட்டுமே செல்லுபடியாகும். இதேபோல், என்ற செங்குத்தாக வீசப்பட்ட பொருளின் அதிகபட்ச உயரத்துக்கான சமன்பாடு சிறிய வேகத்துக்கும் சிறிய தூரத்துக்கும் மட்டுமே பயன்படுத்தலாம்.
ஈர்ப்பு மற்றும் வானியல்
தொகுநமது சூரிய குடும்பத்தில் உள்ள கிரகங்கள், சூரியனின் எடை, நட்சத்திரங்கள் தூரம், குவாசார்கள் மற்றும் இருண்ட பொருள் பற்றி விரிவான தகவல்களை நியூட்டனின் ஈர்ப்பு விதி தெரிவிக்கிறது. நாம் அனைத்து கோள்கள் அல்லது சூரியனுக்கு பயணம் செய்தது இல்லை என்றாலும், அவற்றின் எடை தெரியும். கோளப்பாதையின் பண்புகளில் ஈர்ப்பு விதிகளை பயன்படுத்துவதன் மூலம் இந்த எடை அளவிடப்படுகிறது. விண்வெளியில் ஒரு பொருள் தனது சுற்றுப்பாதையை தக்க வைத்து கொள்கிறது ஏனெனில் அதன் மேல் ஈர்ப்பு விசை செயல்படுகிறது. கோள்கள் நட்சத்திரங்களை சுற்றும், நட்சத்திரங்கள் விண்மீன் திரள் மையத்தை சுற்றும், விண்மீன் திரள்கள் அதன் நிறை மையத்தை சுற்றும், க்ளஸ்தர்கள்சூப்பர்க்லச்டரை சுற்றும். ஒரு பொருள் மற்றொரு பொருள் மீது செலுத்திய ஈர்ப்பு சக்தி அந்த பொருட்களின் எடைக்கு நேர் விகிதத்திலும் மற்றும் அவர்களுக்கு இடையே உள்ள தூரம் சதுர எதிர் விகிதாசாரத்தில் இருக்கும்.
ஈர்ப்பு கதிர்வீச்சு
தொகுபொது சார்பியல், ஈர்ப்பு கதிர்வீச்சு காலவெளியின் வளைவு இணை சுற்றுவட்ட பாதை பொருட்களை கொண்டு இருப்பது போன்ற, ஊசலாடும் அமைந்துள்ள சூழ்நிலையில் உருவாக்கப்பட்டது. சூரிய குடும்பத்தில் உமிழப்படும் ஈர்ப்பு கதிர்வீச்சு அளவிடுவதற்கு மிகவும் சிறியதாக உள்ளது. எனினும், ஈர்ப்பு கதிர்வீச்சு பைனரி பல்சர் அமைப்புகளில் PSR B1913 +16 காலப்போக்கில் ஏற்படும் ஒரு ஆற்றல் இழப்பு என மறைமுகமாக கண்டறியப்பட்டுள்ளது. நியூட்ரான் நட்சத்திரம் சேர்க்கை மற்றும் கருங்குழி உருவாக்கம் ஈர்ப்பு கதிர்வீச்சு கண்டறியும் அளவு உருவாக்கலாம் என்று நம்பப்படுகிறது. LIGO போன்ற ஈர்ப்பு கதிர்வீச்சு ஆய்வுக்கூடங்கள் சிக்கலை ஆய்வு செய்கின்றன. எந்த ஒரு உறுதி கண்டறிதல்களையும் இந்த கருதுகோள் கதிரியக்கத்தின் மூலம் செய்யப்படவில்லை, ஆனால் LIGO பின்னால் உள்ள அறிவியல் செம்மைப்படுத்தபட்டுள்ளது மற்றும் கருவிகளுக்கு அதிக உணர்திறன் அடுத்த தசாப்தத்தில் வழங்கப்பட்டுள்ளது. .
சிக்கல்கள் மற்றும் முரண்பாடுகள்
தொகுஈர்ப்பு சிறந்த கோட்பாடுகள் தேவை சுட்டி அல்லது ஒருவேளை வேறு வழிகளில் விளக்கலாம் இது போதுமான அளவு கணக்கில் இல்லை என்று சில அவதானிப்புகள், உள்ளன.

- அதிவேக நட்சத்திரங்கள்: விண்மீன்மண்டலங்களிலும் வெளிப்பகுதியில் உள்ள நட்சத்திரங்கள் வேகமாக நகரும்படி நட்சத்திரங்களின் திசைவேகங்கள் ஒரு பரவலாக பிரிக்கப்படிருக்கும் . க்ளுச்டேரில் உள்ள நட்சத்திர மண்டலங்கள், அதே மாதிரி காட்டியது. இருண்ட பொருள் மின்காந்த வாயிலாக அல்லாமல் ஈர்ப்பினால் தொடர்பு கொள்வது முரண்பாடாக இருக்கிறது. நியூட்டனின் இயக்கவியல் பல்வேறு மாற்றங்களை கூட முன்மொழியப்பட்டுள்ளன.
- பயணங்களின் ஒழுங்கின்மை : பல்வேறு விண்கலம் ஈர்ப்பு சூழ்ச்சி உதவிய போது எதிர்பார்த்ததை விட அதிக முடுக்கம் ஏற்பட்டுள்ளது.
- விரிவாக்கம் முடுக்கி: வெளியின் அளவியல் விரிவாக்கம் வேகமாக தோன்றுகிறது. இதற்கு விளக்கம் அளிக்க இருண்ட சக்தி முன்மொழியப்பட்டுள்ளது.
- வானியல் அலகின் முரணான அதிகரிப்பு: அண்மைய அளவீடுகள் கோள்களின் கோளப்பாதைகள் வேகமாக விரிவடைவதை சூரியனின் எடை ஆற்றலை வெளிவிடுவதன் மூலம் குறைவதை காட்டுகிறது.
- கூடுதல் ஆற்றல் கொண்ட ஃபோட்டான்கள்: ஃபோட்டான்கள் மண்டலம் கொத்தாக பயணிக்கும் பொது ஆற்றலை பெறவும் பின்னர் வழியில் மீண்டும் அதை இழக்கவும் வேண்டும். ஃபோட்டான்கள் ஆற்றலை திரும்பி அனுப்புவதைபிரபஞ்சத்தின் முடுக்கி விரிவாக்கம் நிறுத்த வேண்டும். இது ஈர்ப்பு எதிர்மறை சதுர விதியை விட குறிப்பிட்ட தூர அளவுகளில் வேகமாக குறைவதை சுட்டிக்காட்டலாம்.
- இருண்ட ஓட்டம்: அண்டத்தின் இயக்கத்தை ஆய்வுகளின் புலப்படாத எடையை நோக்கி ஒரு மர்ம இருண்ட ஓட்டம் இருப்பதை கண்டிருக்கிறோம். பிக் ேங் தற்போதைய மாதிரிகள் பயன்படுத்தி அந்த ஈர்ப்பு குறிப்பிட்ட தூர அளவுகளில் தலைகீழ்-ஸ்கொயர் விட மெதுவாக குறையும் என்பதை என்பதால் இது போன்ற ஒரு பெரிய எடை சேர்ந்திருப்பது மிகவும் பெரியதாக உள்ளது.
- கூடுதல் எடை உடைய ஹைட்ரஜன் மேகங்கள்: லைமேன்-ஆல்பா காட்டின் நிறமாலை வரிகள் ஹைட்ரஜன் மேகங்கள் மேலும் எதிர்பார்க்கப்படும் குறிப்பிட்ட அளவுகளில் ஒன்றாக தடிமனாகின்றன மற்றும், இருண்ட ஓட்டம் போல், அந்த ஈர்ப்பு குறிப்பிட்ட தூரத்தை அளவுகளில் ஆஃப் தலைகீழ்-ஸ்கொயர் விட மெதுவாக விழும் குறிக்கலாம் என்று.
மாற்று தத்துவங்கள்
தொகுவரலாற்று மாற்று தத்துவங்கள்
தொகு- அரிஸ்டாட்டிலின் புவியீர்ப்பு தத்துவம்
- le சேஜ் ஈர்ப்பு கோட்பாடு (1784)(LeSage ஈர்ப்பு என்றும்) திரவம் சார்ந்த விளக்க அடிப்படையில் ஒரு ஒளி வாயு முழு பிரபஞ்சத்தை நிரப்புயுள்ளதை ஜார்ஜ் லூயிஸ் லு முனிவர் முன்மொழிந்தார். .
- ஈர்ப்பு ரிட்ஸ் கோட்பாடு, ஆன். கெம். பிசிக்ஸ். 13, 145, (1908) பக் 267-271, வெபர்-காஸ் மின்னியக்கவிசையியல் ஈர்ப்பு பயன்படுத்தப்படும். சிறுமை வீச்சு பாரம்பரிய முன்னேற்றம்.
- ஈர்ப்பு Nordström கோட்பாடு (1912, 1913), பொது சார்பியல் முந்தைய போட்டியாளர்.
- ஈர்ப்பு ஒயிட்ஹெட் கோட்பாடு (1922), பொது சார்பியல் மற்றொரு ஆரம்ப போட்டியாளர்.
சமீபத்திய மாற்று தத்துவங்கள்
தொகு- Brans-Dicke புவியீர்ப்பு கோட்பாடு (1961)
- தூண்டிய ஈர்ப்பு (1967), பொது சார்பியல் விஷயம் குவாண்டம் தள கோட்பாடுகளில் இருந்து எழும் என்று ஆண்ட்ரி Sakharov எண்ணினார்.
- திருத்திய நியூட்டனின் இயக்கவியல் (மோண்ட்) (1981), Mordehai Milgrom சிறிய முடுக்கத்திற்கு நியூட்டனின் இரண்டாம் இயக்க சட்டம் ஒரு மாற்றத்தை முன்மொழிந்தார்.
- ஜான் Moffat மூலம் Nonsymmetric ஈர்ப்பு கோட்பாடு (NGT) (1994)
- பண்புரு-வெக்டார் ஸ்கேலார் ஈர்ப்பு (TeVeS) (2004), ஜேக்கப் Bekenstein மூலம் மோண்ட் ஒரு சார்பு மாற்றம்
- ஒரு entropic சக்தியாக ஈர்ப்பு, எண்ட்ரோப்பியின் வெப்பவியக்கவியல் கருத்து இருந்து ஒரு அவசர நிகழ்வு என எழும் ஈர்ப்பு.
- Superfluid வெற்றிடம் கோட்பாடு ஈர்ப்பு கால வளைந்த superfluid சார்பின்மை பின்னணி ஒரு கூட்டு கிளர்வு முறைமை எழுகின்றன.
காண்க
தொகு- விடுபடும் வேகம், குறைந்த வேகம் ஒரு ஈர்ப்பு இருந்து தப்பிக்க தேவை
- நியூட்டனின் இயக்க விதிகள்
- வளைவுந்தம்
- ஈர்ப்பு அலை
- கெப்லரின் கோள் இயக்க விதிகள்
- லெக்ராஞ்சியப் புள்ளி
- திட்ட புவியீர்ப்பு முடுக்கம்
மேற்கோள்கள்
தொகு- ↑ Ball, Phil (June 2005). "Tall Tales". Nature News. doi:10.1038/news050613-10.
- ↑ கலீலியோ கலிலி (1638), Two New Sciences, First Day Salviati speaks: "If this were what Aristotle meant you would burden him with another error which would amount to a falsehood; because, since there is no such sheer height available on earth, it is clear that Aristotle could not have made the experiment; yet he wishes to give us the impression of his having performed it when he speaks of such an effect as one which we see."
வெளி இணைப்புகள்
தொகு- Hazewinkel, Michiel, ed. (2001), "Gravitation", Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104
- Hazewinkel, Michiel, ed. (2001), "Gravitation, theory of", Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண் 978-1556080104


