விக்கிப்பீடியா

மெர்சென் பகா எண்கள்-செவ்விய எண்கள் பட்டியல்

விக்கிப்பீடியா:பட்டியலிடல்

எண்கோட்பாட்டில், மெர்சென் பகாஎண்களும் செவ்விய எண்களும் ஒன்றுக்கொன்று ஆழமான தொடர்புடைய இருவிதமான இயல் எண்களாகும்.

Cuisenaire rods showing the proper divisors of 6 (1, 2, and 3) adding up to 6
6, ஒரு செவ்விய எண் என்பதற்கான விளக்கப்படம்
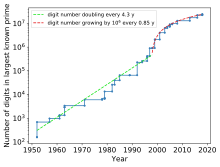
A graph plotting years on the x-axis with the number of digits of the largest known prime logarithmically on the y-axis, with two trendlines
ஆண்டுவாரியாக அறியப்பட்ட மிகப்பெரிய பகாஎண்கள் ஒவ்வொன்றின் இலக்கங்களின் எண்ணிக்கையைக் காட்டும் மடக்கை வரைபடம். இவை அனைத்துமே கிட்டத்தட்ட மெர்சென் பகாஎண்களாகும்.
மெர்சென் பகாத்தனிகள் (மெர்சென் பகாஎண்கள்)

"மாரின் மெர்சென்" எனும் பிரெஞ்சு அறிவியலாளரின் பெயரால் அழைக்கப்படும் இவ்வெண்கள்,

2p − 1 , (ஒரு நேர்ம முழுவெண்) என்ற வடிவில் எழுதக்கூடிய பகாஎண்களாகும்.

எடுத்துக்காட்டாக,

22 − 1 = 3 என்ற வடிவில் எழுதக்கூடியதாக பகா எண் '3' உள்ளதால், '3' ஒரு மெர்சென் பகாஎண்ணாகும்.[1][2]

இவ்வடிவிலமையும் எண்கள் மெர்சென் பகா எண்களாக இருப்பதற்கு p உம் ஒரு பகா எண்ணாக இருக்க வேண்டும். ஆனால் p இன் அனைத்து பகா எண் மதிப்புகளுக்கும், 2p − 1 வடிவிலமையும் அனைத்து எண்களும், பகா எண்களாக இருப்பதில்லை; எனவே அவை மெர்சென் பகாஎண்களுமல்ல. எடுத்துக்காட்டாக,

23 − 1 = 7 . இது ஒரு பகா எண்; மேலும் மெர்சென் பகா எண்ணுங்கூட; ஆனால்,
211 − 1 = 2047 = 23 × 89 பகா எண் அல்ல.[3]
"செவ்விய எண்கள்"

தமது தகு வகுஎண்களின் கூட்டுத்தொகைக்குச் சமமாகவுள்ள இயல் எண்கள் செவ்விய எண்கள் அல்லது நிறைவெண்கள் எனப்படும்.

எடுத்துக்காட்டாக:

6 ஒரு செவ்விய எண்; அதன் தகு வகுஎண்கள் 6 are 1, 2, 3. இவற்றின் கூட்டுதொகை 1 + 2 + 3 = 6.[2][4]

மெர்சென் பகாஎண்களுக்கும் இரட்டைச் செவ்விய எண்களுக்குமிடையே ஓர் ஒன்றுக்கு-ஒன்று தொடர்பு உள்ளது. இத்தொடர்பின் ஒரு பகுதி யூக்ளிடாலும், பின்னர் அவரைத் தொடர்ந்து அதன் அடுத்தபகுதி ஆய்லராலும் நிறுவப்பட்டன. இத்தொடர்பு, யூக்ளிடு-ஆய்லர் தேற்றம் என அழைக்கப்படுகிறது:

தொடர்பு
"ஓர் இரட்டையெண்ணானது 2p−1(2p − 1) (இதில், 2p − 1 ஒரு மெர்சென் பகாஎண்) என்ற வடிவில் "இருந்தால், இருந்தால் மட்டுமே", அந்த இரட்டையெண் ஒரு செவ்விய எண்ணாக இருக்கமுடியும்."

எடுத்துக்காட்டாக:

p = 2, 22 − 1 = 3 இரண்டும் பகாஎண்கள்;
மேலும், 22 − 1 × (22 − 1) = 2 × 3 = 6 என்ற செவ்விய எண்ணாக உள்ளதைக் காணலாம்.[1][5][6]

மெர்சென் பகாஎண்கள், இரட்டைச் செவ்விய எண்கள் ஆகிய இரண்டினது எண்ணிக்கைகளும் முடிவுற்றதா அல்லது முடிவற்றதா என்பது ஒரு விடையறிப்படாக் கேள்வியாகவே இதுவரை உள்ளது.[2][6]"இலென்சுட்ரா-பொமெரான்சு-வாக்சுடாஃப் அனுமானம்", மெர்சென் பகாஎண்களின் எண்ணிக்கை பற்றியதாகும். இவ்வனுமானத்தின்படி, x ஐ விடச் சிறிய மெர்சென் பகாஎண்களின் எண்ணிக்கையானது (eγ / log 2) × log log x ஆகும். இதிலுள்ள e ஆனது ஆய்லரின் எண்; γ ஆனது "ஆய்லரின் மாறிலி"; log ஆனது இயல் மடக்கை.[7][8][9] மேலும் ஒற்றைச் செவ்விய எண்கள் உள்ளனவா என்பதும் விடை அறியப்படாதச் சிக்கலாகவே உள்ளது; ஒருவேளை ஏதாவது ஒற்றைச் செவ்விய எண் இருக்குமாயின் அவற்றுக்கான நிபந்தனைகள் பல கண்டறியப்பட்டுள்ளன. ஒற்றைச் செவ்விய எண் இருந்தால், அது குறைந்தபட்சம் 101500 ஆக இருக்கும் என்பதே அத்தகைய நிபந்தனைகளுள் ஒன்று.[10]

கீழுள்ள பட்டியல் தற்போதுவரை கண்டுபிடிக்கப்பட்ட மெர்சென் பகாஎண்கள், செவ்விய எண்கள் இரண்டையும் அவற்றுக்குரிய அடுக்கெண் p உடன் தருகிறது. 2023 நிலவரப்படி, 51 மெர்சென் பகாஎண்கள் (எனவே 51 செவ்விய எண்கள்) கண்டுபிடிக்கப்பட்டுள்ளன. அவற்றுள் மிகப்பெரிய 17 மெர்சென் பாகாஎண்கள் "பகிர்வு கணித்தல் திட்டத்தின்" கீழமைந்த இணையவழி மெர்சென் பெருந்தேடல்-“கிம்ப்” (Great Internet Mersenne Prime Search-GIMPS) மூலம் கண்டறியப்பட்டன.[2] மேலும், புதிய மெர்சென் பகாஎண்கள், "இலூகாசு- இலேமர் மெய்த்தேர்வு" (LLT) மூலமாகவும் கண்டறியப்பட்டன.[2]

2022 வரை கண்டறியப்பட்ட நிலவரப்படி , அட்டவணையிலுள்ள தர எண்கள் தரப்பட்டுள்ளன. வேறு சிறிய மெர்சென் பகாஎண்கள் கண்டுபிடிக்கப்பட்டால், அதற்கேற்றாற்போல தரஎண்கள் மாறவும் வாய்ப்புள்ளது. "மிகப்பெரிய இணைய மெர்சென் பகாஎண் தேடல்" திட்டத்தின்படி, 2024 வரையிலான, 48 ஆவது அடுக்கெண் p = 57,885,161 க்குக் கீழுள்ளவை அனைத்தும் சரிபார்க்கப்பட்டுவிட்டன.[11] யூக்ளிடு-ஆய்லர் தேற்றத்தின்படி, மெர்சென் பகாஎண்களுக்குரிய கண்டுபிடிக்கப்பட்ட ஆண்டும் கண்டுபிடித்தவர்களும், செவ்விய எண்களுக்கும் பொருந்தும். அட்டவணையின் இறுதியில் இடம்பெறும் எண்கள் மிகவும் அதிக நீளமானவை என்பதால், அவற்றின் முதல் ஆறு இலக்கங்களும் கடைசி ஆறு இலக்கங்களும் மட்டுமே காட்டப்பட்டுள்ளன.

பட்டியல்

தொகு
அறியப்பட்ட 51 மெர்சென் பகாஎண்களும், அவற்றுக்குரிய செவ்விய எண்களும் அடங்கிய பட்டியல்
தரம் p மெர்சென் பகாஎண் மெர்சென் பகாஎண் இலக்கங்கள் செவ்விய எண் செவ்விய எண் இலக்கங்கள் கண்டுபிடிக்கப்பட்ட காலம் கண்டுபிடிப்பாளர் முறை சான்று[12]
1 2 3 1 6 1 பண்டைக்காலம்[a] பண்டைய கிரேக்கக் கணிதவியலாளர்களால் அறியப்பட்டிருந்தது. பதிவு செய்யப்படவில்லை [13][14][15]
2 3 7 1 28 2 [13][14][15]
3 5 31 2 496 3 [13][14][15]
4 7 127 3 8128 4 [13][14][15]
5 13 8191 4 33550336 8 1200s/c. 1456[b] பலர்[c] சோதனை வகுத்தல் [14][15]
6 17 131071 6 8589869056 10 1588[b] பியட்ரொ கேட்டால்டி [2][17]
7 19 524287 6 137438691328 12 [2][17]
8 31 2147483647 10 230584...952128 19 1772 லியோனார்டு ஆய்லர் கட்டுப்பாடுகளுடன் கூடிய சோதனை வகுத்தல் [18][19]
9 61 230584...693951 19 265845...842176 37 நவம்பர் 1883 இவான் பெரூசின் லூகாசு தொடர்வரிசைகள் [20]
10 89 618970...562111 27 191561...169216 54 சூன் 1911 இரால்ப் எர்னசுட் பவர்சு [21]
11 107 162259...288127 33 131640...728128 65 சூன் 1, 1914 [22]
12 127 170141...105727 39 144740...152128 77 சனவரி 10, 1876 எட்வர்டு லூகாசு [23]
13 521 686479...057151 157 235627...646976 314 சனவரி 30, 1952 இரபேல் எம். இராபின்சன் LLT (SWAC கணினி) [24]
14 607 531137...728127 183 141053...328128 366 [24]
15 1,279 104079...729087 386 541625...291328 770 சூன் 25, 1952 [25]
16 2,203 147597...771007 664 108925...782528 1,327 அக்டோபர் 7, 1952 [26]
17 2,281 446087...836351 687 994970...915776 1,373 அக்டோபர் 9, 1952 [26]
18 3,217 259117...315071 969 335708...525056 1,937 செப்டம்பர் 8, 1957 ஹன்சு ரீசல் LLT (BESK-கணினி) [27]
19 4,253 190797...484991 1,281 182017...377536 2,561 நவம்பர் 3, 1961 அலெக்சான்டர் ஹுர்விட்சு LLT (IBM 7090 கணினி) [28]
20 4,423 285542...580607 1,332 407672...534528 2,663 [28]
21 9,689 478220...754111 2,917 114347...577216 5,834 மே 11, 1963 டொனால்டு பி. கில்லீசு LLT (ILLIAC II கணினி) [29]
22 9,941 346088...463551 2,993 598885...496576 5,985 மே 16, 1963 [29]
23 11,213 281411...392191 3,376 395961...086336 6,751 சூன் 2, 1963 [29]
24 19,937 431542...041471 6,002 931144...942656 12,003 மார்ச்சு 4, 1971 பிரயன்ட் டக்கர்மேன் LLT (IBM 360/91 கணினி) [30]
25 21,701 448679...882751 6,533 100656...605376 13,066 அக்டோபர் 30, 1978 லன்டன் கர்ட் நோல் & லாரா நிக்கல் LLT (CDC Cyber 174 கணினி) [31]
26 23,209 402874...264511 6,987 811537...666816 13,973 பெப்ரவரி 9, 1979 லன்டன் கர்ட் நோல் [31]
27 44,497 854509...228671 13,395 365093...827456 26,790 ஏப்ரல் 8, 1979 ஹாரி எல். நெல்சன் & டேவிட் சுலோவின்சுகி LLT (Cray-1 கணினி) [32][33]
28 86,243 536927...438207 25,962 144145...406528 51,924 செப்டம்பர் 25, 1982 டேவிட் சுலோவின்சுகி [34]
29 110,503 521928...515007 33,265 136204...862528 66,530 சனவரி 29, 1988 வால்டர் கோல்க்கிட் & லூக் வெல்ஷ் LLT (NEC SX-2 கணினி) [35][36]
30 132,049 512740...061311 39,751 131451...550016 79,502 செப்டம்பர் 19, 1983 டேவிட் சுலோவின்சுகி LLT (Cray X-MP கணினி) [37]
31 216,091 746093...528447 65,050 278327...880128 130,100 செப்டம்பர் 1, 1985 LLT (Cray X-MP/24 கணினி) [38][39]
32 756,839 174135...677887 227,832 151616...731328 455,663 பெப்ரவரி 17, 1992 LLT (ஹார்வெல் சோதனைக் கூடத்தின் Cray-2 கணினி) [40]
33 859,433 129498...142591 258,716 838488...167936 517,430 சனவரி 4, 1994 LLT (Cray C90 கணினி) [41]
34 1,257,787 412245...366527 378,632 849732...704128 757,263 செப்டம்பர் 3, 1996 LLT (Cray T94 கணினி) [42][43]
35 1,398,269 814717...315711 420,921 331882...375616 841,842 நவம்பர் 13, 1996 GIMPS / ஜோயல் ஆர்மென்காடு LLT / பிரைம்95 (90 MHz பென்ட்டியம் கணினி) [44]
36 2,976,221 623340...201151 895,932 194276...462976 1,791,864 ஆகத்து 24, 1997 GIMPS / கோர்டன் இசுபென்சு LLT / பிரைம்95 (100 MHz பென்ட்டியம் கணினி) [45]
37 3,021,377 127411...694271 909,526 811686...457856 1,819,050 சனவரி 27, 1998 GIMPS / உரோலன்டு கிளார்க்சன் LLT / பிரைம்95 (200 MHz பென்டியம் கணினி) [46]
38 6,972,593 437075...193791 2,098,960 955176...572736 4,197,919 சூன் 1, 1999 GIMPS / நாரயண் ஹஜ்ரத்வாலா LLT / பிரைம்95 (IBM Aptiva -350 MHz பென்டியம் II]] [47]
39 13,466,917 924947...259071 4,053,946 427764...021056 8,107,892 நவம்பர் 14, 2001 GIMPS / மைக்கேல் கேமரான் LLT / பிரைம்95 (800 MHz அத்லோன் டி-பெர்டு (2000–2001) [48]
40 20,996,011 125976...682047 6,320,430 793508...896128 12,640,858 நவம்பர் 17, 2003 GIMPS / மைக்கேல் ஷேஃப்பர் LLT / பிரைம்95 (டென் டைமென்ஷன் 2 GHz பென்டியம் 4 கணினி) [49]
41 24,036,583 299410...969407 7,235,733 448233...950528 14,471,465 மே 15, 2004 GIMPS / ஜோஷ் பின்டிலி LLT / பிரைம்95 (2.4 GHz பென்ட்டியம் 4 கணினி) [50]
42 25,964,951 122164...077247 7,816,230 746209...088128 15,632,458 பெப்ரவரி 18, 2005 GIMPS / மார்டின் நோவாக் [51]
43 30,402,457 315416...943871 9,152,052 497437...704256 18,304,103 திசம்பர் 15, 2005 GIMPS / கர்ட்டிசு கூப்பர் & இசுடீவன் பூன் LLT / பிரைம்95 (மத்திய மிசௌரி பல்கலைக்கழகம்) [52]
44 32,582,657 124575...967871 9,808,358 775946...120256 19,616,714 செப்டம்பர் 4, 2006 [53]
45 37,156,667 202254...220927 11,185,272 204534...480128 22,370,543 செப்டம்பர் 6, 2008 GIMPS / கான்ஸ்-மைக்கேல் எல்வெனிச் LLT / பிரைம்95 (கணினி) [54]
46 42,643,801 169873...314751 12,837,064 144285...253376 25,674,127 சூன் 4, 2009[d] GIMPS / ஆட் மாக்னர் இசுட்ரின்டுமோ LLT / பிரைம்95 (3 GHz இன்டல் கோர்-கணினி) [55]
47 43,112,609 316470...152511 12,978,189 500767...378816 25,956,377 ஆகத்து 23, 2008 GIMPS /எட்சன் இசுமித் LLT / பிரைம்95 (டெல் ஆப்டிபிளக்சு இன்டல் கோர் 2 டூயோ E6600-கணினி) [54][56][57]
48 57,885,161 581887...285951 17,425,170 169296...130176 34,850,340 சனவரி 25, 2013 GIMPS / கர்ட்டிசு கூப்பர் LLT / பிரைம்95 (மத்திய மிசௌரி பல்கலைக்கழகக் கணினி) [58][59]
* 68,029,391 சரிபார்க்கப்படாத மிகச்சிறியது[e]
49[f] 74,207,281 300376...436351 22,338,618 451129...315776 44,677,235 சனவரி 7, 2016[g] GIMPS / கர்டிசு கூப்பர் LLT / பிரைம்95 - இன்டல்கோர் i7-4790 கணினி [60][61]
50[f] 77,232,917 467333...179071 23,249,425 109200...301056 46,498,850 திசம்பர் 26, 2017 GIMPS / ஜோனாதன் பேஸ் LLT / பிரைம்95 -இண்டல் கோர் i5-6600 கணினி [62][63]
51[f] 82,589,933 148894...902591 24,862,048 110847...207936 49,724,095 திசம்பர் 7, 2018 GIMPS / பேட்ரிக் லாரோச் LLT / பிரைம்95 - இன்டல் கோர் i5-4590T கணினி [64][65]
* 116,167,187 சோதிக்கப்படாத மிகச்சிறியது[e]

குறிப்புகள்

தொகு
  1. ↑ The first four perfect numbers were documented by Nicomachus circa 100, and the concept was known (along with corresponding Mersenne primes) to Euclid at the time of his Elements. There is no record of discovery.
  2. ↑ 2.0 2.1 Islamic mathematicians such as Ismail ibn Ibrahim ibn Fallus (1194–1239) may have known of the fifth through seventh perfect numbers prior to European records.[16]
  3. ↑ Found in an anonymous manuscript, Codex latinus monacensis -
  4. ↑ M42,643,801 was first reported to GIMPS on April 12, 2009 but was not noticed by a human until June 4, 2009 due to a server error.
  5. ↑ 5.0 5.1 As of 27 ஏப்ரல் 2024[11]
  6. ↑ 6.0 6.1 6.2 It has not been verified whether any undiscovered Mersenne primes exist between the 48th (M57,885,161) and the 51st (M82,589,933) on this table; the ranking is therefore provisional.
  7. ↑ M74,207,281 was first reported to GIMPS on September 17, 2015 but was not noticed by a human until January 7, 2016 due to a server error.

மேற்கோள்கள்

தொகு
  1. ↑ 1.0 1.1 Stillwell, John (2010). Mathematics and Its History. Undergraduate Texts in Mathematics. இசுபிரிங்கர் பதிப்பகம். p. 40. பன்னாட்டுத் தரப்புத்தக எண் 978-1-4419-6052-8. Archived from the original on 13 October 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 Caldwell, Chris K. "Mersenne Primes: History, Theorems and Lists". PrimePages. Archived from the original on 4 October 2021. பார்க்கப்பட்ட நாள் 4 October 2021.
  3. ↑ Caldwell, Chris K. "If 2n-1 is prime, then so is n". PrimePages. Archived from the original on 5 October 2021. பார்க்கப்பட்ட நாள் 12 October 2021.
  4. ↑ Prielipp, Robert W. (1970). "Perfect Numbers, Abundant Numbers, and Deficient Numbers". The Mathematics Teacher 63 (8): 692–96. doi:10.5951/MT.63.8.0692. http://www.jstor.org/stable/27958492. பார்த்த நாள்: 13 October 2021. 
  5. ↑ Caldwell, Chris K. "Characterizing all even perfect numbers". PrimePages. Archived from the original on 8 October 2014. பார்க்கப்பட்ட நாள் 12 October 2021.
  6. ↑ 6.0 6.1 Crilly, Tony (2007). "Perfect numbers". 50 mathematical ideas you really need to know. Quercus Publishing. பன்னாட்டுத் தரப்புத்தக எண் 978-1-84724-008-8. Archived from the original on 13 October 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  7. ↑ Caldwell, Chris K. "Heuristics Model for the Distribution of Mersennes". PrimePages. Archived from the original on 5 October 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  8. ↑ Samuel S. Wagstaff Jr. (January 1983). "Divisors of Mersenne numbers" (in en). Mathematics of Computation 40 (161): 385–397. doi:10.1090/S0025-5718-1983-0679454-X. பன்னாட்டுத் தர தொடர் எண்:0025-5718. http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-1983-0679454-X. 
  9. ↑ Carl Pomerance (September 1981). "Recent developments in primality testing" (in en). The Mathematical Intelligencer 3 (3): 97–105. doi:10.1007/BF03022861. பன்னாட்டுத் தர தொடர் எண்:0343-6993. https://link.springer.com/content/pdf/10.1007/BF03022861.pdf. 
  10. ↑ Ochem, Pascal; Rao, Michaël (30 January 2012). "Odd perfect numbers are greater than 101500" (in en). Mathematics of Computation 81 (279): 1869–1877. doi:10.1090/S0025-5718-2012-02563-4. பன்னாட்டுத் தர தொடர் எண்:0025-5718. http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-2012-02563-4. 
  11. ↑ 11.0 11.1 "GIMPS Milestones Report". Great Internet Mersenne Prime Search. Archived from the original on 13 October 2021. பார்க்கப்பட்ட நாள் 31 January 2024.
  12. ↑ Sources applying to almost all entries:
  13. ↑ 13.0 13.1 13.2 13.3 Joyce, David E. "Euclid's Elements, Book IX, Proposition 36". mathcs.clarku.edu. Archived from the original on 17 June 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  14. ↑ 14.0 14.1 14.2 14.3 14.4 Dickson, Leonard Eugene (1919). History of the Theory of Numbers, Vol. I. Carnegie Institution of Washington. pp. 4–6.
  15. ↑ 15.0 15.1 15.2 15.3 15.4 Smith, David Eugene (1925). History of Mathematics: Volume II. Dover. p. 21. பன்னாட்டுத் தரப்புத்தக எண் 978-0-486-20430-7.
  16. ↑ O'Connor, John J.; Robertson, Edmund F. "Perfect numbers". MacTutor History of Mathematics archive. Archived from the original on 5 October 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  17. ↑ 17.0 17.1 Cataldi, Pietro Antonio (1603). Trattato de' numeri perfetti di Pietro Antonio Cataldo [Pietro Antonio Cataldi's treatise on perfect numbers] (in இத்தாலியன்). Presso di Heredi di Giouanni Rossi.
  18. ↑ Caldwell, Chris K. "Modular restrictions on Mersenne divisors". PrimePages. பார்க்கப்பட்ட நாள் 22 November 2021.
  19. ↑ Leonhard Euler (1772). "Extrait d'un lettre de M. Euler le pere à M. Bernoulli concernant le Mémoire imprimé parmi ceux de 1771, p 318" (in fr). Nouveaux Mémoires de l'académie royale des sciences de Berlin 1772: 35–36. https://scholarlycommons.pacific.edu/cgi/viewcontent.cgi?article=1460&context=euler-works. பார்த்த நாள்: 13 October 2021. 
  20. ↑ "Sur un nouveau nombre premier, annoncé par le père Pervouchine" (in fr). Bulletin de l'Académie impériale des sciences de St.-Pétersbourg 31: 532–533. 27 January 1887. https://www.biodiversitylibrary.org/page/34669913. பார்த்த நாள்: 13 October 2021. 
  21. ↑ Ralph Ernest Powers (November 1911). "The Tenth Perfect Number". The American Mathematical Monthly 18 (11): 195–197. doi:10.2307/2972574. 
  22. ↑ "Records of Proceedings at Meetings". Proceedings of the London Mathematical Society s2-13 (1): iv-xl. 1914. doi:10.1112/plms/s2-13.1.1-s. 
  23. ↑ Édouard Lucas (1876). "Note sur l'application des séries récurrentes à la recherche de la loi de distribution des nombres premiers" (in fr). Comptes rendus de l'Académie des Sciences 82: 165–167. http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-3039&I=166&M=tdm. பார்த்த நாள்: 13 October 2021. 
  24. ↑ 24.0 24.1 "Notes" (in en). Mathematics of Computation 6 (37): 58–61. January 1952. doi:10.1090/S0025-5718-52-99405-2. பன்னாட்டுத் தர தொடர் எண்:0025-5718. https://www.ams.org/mcom/1952-06-037/S0025-5718-52-99405-2/. பார்த்த நாள்: 13 October 2021. 
  25. ↑ "Notes" (in en). Mathematics of Computation 6 (39): 204–205. July 1952. doi:10.1090/S0025-5718-52-99389-7. பன்னாட்டுத் தர தொடர் எண்:0025-5718. http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-52-99389-7. 
  26. ↑ 26.0 26.1 "Notes" (in en). Mathematics of Computation 7 (41): 67–72. January 1953. doi:10.1090/S0025-5718-53-99372-7. பன்னாட்டுத் தர தொடர் எண்:0025-5718. https://www.ams.org/mcom/1953-07-041/S0025-5718-53-99372-7/. 
  27. ↑ Hans Riesel (January 1958). "A New Mersenne Prime". Mathematics of Computation 12 (61): 60. doi:10.1090/S0025-5718-58-99282-2. https://www.ams.org/journals/mcom/1958-12-061/S0025-5718-58-99282-2/. 
  28. ↑ 28.0 28.1 Hurwitz, Alexander (April 1962). "New Mersenne primes" (in en). Mathematics of Computation 16 (78): 249–251. doi:10.1090/S0025-5718-1962-0146162-X. பன்னாட்டுத் தர தொடர் எண்:0025-5718. http://www.ams.org/jourcgi/jour-getitem?pii=S0025-5718-1962-0146162-X. 
  29. ↑ 29.0 29.1 29.2 Donald B. Gillies (January 1964). "Three new Mersenne primes and a statistical theory". Mathematics of Computation 18 (85): 93–97. doi:10.1090/S0025-5718-1964-0159774-6. https://archive.org/details/sim_mathematics-of-computation_1964-01_18_85/page/93. 
  30. ↑ Bryant Tuckerman (October 1971). "The 24th Mersenne Prime". Proceedings of the National Academy of Sciences 68 (10): 2319–2320. doi:10.1073/pnas.68.10.2319. பப்மெட்:16591945. Bibcode: 1971PNAS...68.2319T. 
  31. ↑ 31.0 31.1 Landon Curt Noll; Nickel, Laura (October 1980). "The 25th and 26th Mersenne primes". Mathematics of Computation 35 (152): 1387. doi:10.1090/S0025-5718-1980-0583517-4. https://archive.org/details/sim_mathematics-of-computation_1980-10_35_152/page/1387. 
  32. ↑ David Slowinski (1978). "Searching for the 27th Mersenne prime". Journal of Recreational Mathematics 11 (4): 258–261. 
  33. ↑ "Science Watch: A New Prime Number". த நியூயார்க் டைம்ஸ். 5 June 1979. https://www.nytimes.com/1979/06/05/archives/science-watch-atmosphere-endangered-a-new-prime-number-great-salt.html. 
  34. ↑ "Announcements" (in en). The Mathematical Intelligencer 5 (1): 60. March 1983. doi:10.1007/BF03023507. பன்னாட்டுத் தர தொடர் எண்:0343-6993. http://link.springer.com/10.1007/BF03023507. 
  35. ↑ Peterson, I. (6 February 1988). "Priming for a Lucky Strike". Science News 133 (6): 85. doi:10.2307/3972461. 
  36. ↑ Colquitt, W. N.; Welsh, L. (April 1991). "A new Mersenne prime". Mathematics of Computation 56 (194): 867. doi:10.1090/S0025-5718-1991-1068823-9. Bibcode: 1991MaCom..56..867C. https://archive.org/details/sim_mathematics-of-computation_1991-04_56_194/page/867. 
  37. ↑ "Number is largest prime found yet.". The Globe and Mail. 24 September 1983. ProQuest 386439660. https://www.proquest.com/docview/386439660. 
  38. ↑ Peterson, I. (28 September 1985). "Prime Time for Supercomputers". Science News 128 (13): 199. doi:10.2307/3970245. 
  39. ↑ Dembart, Lee (17 September 1985). "Supercomputer Comes Up With Whopping Prime Number" (in en-US). Los Angeles Times. https://www.latimes.com/archives/la-xpm-1985-09-17-mn-20124-story.html. 
  40. ↑ Maddox, John (26 March 1992). "The endless search for primality" (in en). Nature 356 (6367): 283. doi:10.1038/356283a0. பன்னாட்டுத் தர தொடர் எண்:1476-4687. Bibcode: 1992Natur.356..283M. 
  41. ↑ "Largest Known Prime Number Discovered on Cray Research Supercomputer". PR Newswire. 10 January 1994. https://go.gale.com/ps/i.do?p=ITOF&u=wikipedia&id=GALE%7CA14684654&v=2.1&it=r&sid=bookmark-ITOF&asid=b1d68ed5. 
  42. ↑ Caldwell, Chris K. "A Prime of Record Size! 21257787-1". PrimePages. Archived from the original on 5 October 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  43. ↑ Gillmor, Dan (3 September 1996). "Crunching numbers: Researchers come up with prime math discovery". Knight Ridder. https://link.gale.com/apps/doc/A18635446/ITOF?u=wikipedia&sid=bookmark-ITOF&xid=68c06627. 
  44. ↑ "GIMPS Discovers 35th Mersenne Prime, 21,398,269-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 12 November 1996 இம் மூலத்தில் இருந்து 7 June 2020 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20200607112616/https://www.mersenne.org/primes/?press=M1398269%2F. 
  45. ↑ "GIMPS Discovers 36th Mersenne Prime, 22,976,221-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 1 September 1997 இம் மூலத்தில் இருந்து 7 June 2020 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20200607112618/https://www.mersenne.org/primes/?press=M2976221%2F. 
  46. ↑ "GIMPS Discovers 37th Mersenne Prime, 23,021,377-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 2 February 1998 இம் மூலத்தில் இருந்து 7 June 2020 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20200607112619/https://www.mersenne.org/primes/?press=M3021377%2F. 
  47. ↑ "GIMPS Discovers 38th Mersenne Prime 26,972,593-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 30 June 1999 இம் மூலத்தில் இருந்து 7 June 2020 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20200607112621/https://www.mersenne.org/primes/?press=M6972593%2F. 
  48. ↑ "GIMPS Discovers 39th Mersenne Prime, 213,466,917-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 6 December 2001 இம் மூலத்தில் இருந்து 7 June 2020 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20200607112627/https://www.mersenne.org/primes/?press=M13466917%2F. 
  49. ↑ "GIMPS Discovers 40th Mersenne Prime, 220,996,011-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 2 February 2003 இம் மூலத்தில் இருந்து 7 June 2020 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20200607112628/https://www.mersenne.org/primes/?press=M20996011%2F. 
  50. ↑ "GIMPS Discovers 41st Mersenne Prime, 224,036,583-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 28 May 2004 இம் மூலத்தில் இருந்து 29 January 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210129065814/https://www.mersenne.org/primes/?press=M24036583. 
  51. ↑ "GIMPS Discovers 42nd Mersenne Prime, 225,964,951-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 27 February 2005 இம் மூலத்தில் இருந்து 14 March 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210314035106/https://www.mersenne.org/primes/?press=M25964951. 
  52. ↑ "GIMPS Discovers 43rd Mersenne Prime, 230,402,457-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 24 December 2005 இம் மூலத்தில் இருந்து 14 March 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210314165053/https://www.mersenne.org/primes/?press=M30402457. 
  53. ↑ "GIMPS Discovers 44th Mersenne Prime, 232,582,657-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 11 September 2006 இம் மூலத்தில் இருந்து 26 January 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210126022359/https://www.mersenne.org/primes/?press=M32582657. 
  54. ↑ 54.0 54.1 "GIMPS Discovers 45th and 46th Mersenne Primes, 243,112,609-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 15 September 2008 இம் மூலத்தில் இருந்து 5 October 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20211005213055/https://www.mersenne.org/primes/?press=M43112609. 
  55. ↑ "GIMPS Discovers 47th Mersenne Prime". Great Internet Mersenne Prime Search. 12 April 2009 இம் மூலத்தில் இருந்து 19 February 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210219094118/https://www.mersenne.org/primes/?press=M42643801. 
  56. ↑ Maugh, Thomas H. (27 September 2008). "Rare prime number found". Los Angeles Times இம் மூலத்தில் இருந்து 27 July 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210727064651/https://www.latimes.com/archives/la-xpm-2008-sep-27-sci-prime27-story.html. 
  57. ↑ Smith, Edson. "The UCLA Mersenne Prime". UCLA Mathematics. Archived from the original on 22 November 2021. பார்க்கப்பட்ட நாள் 22 November 2021.
  58. ↑ "GIMPS Discovers 48th Mersenne Prime, 257,885,161-1 is now the Largest Known Prime.". Great Internet Mersenne Prime Search. 5 February 2013 இம் மூலத்தில் இருந்து 26 January 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210126100905/https://www.mersenne.org/primes/?press=M57885161. 
  59. ↑ Yirka, Bob (6 February 2013). "University professor discovers largest prime number to date". phys.org (in ஆங்கிலம்). Archived from the original on 16 January 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  60. ↑ "GIMPS Project Discovers Largest Known Prime Number: 274,207,281-1". Great Internet Mersenne Prime Search. 19 January 2016 இம் மூலத்தில் இருந்து 7 January 2018 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20180107133230/https://www.mersenne.org/primes/?press=M74207281. 
  61. ↑ "Largest known prime number discovered in Missouri" (in en-GB). BBC News. 20 January 2016 இம் மூலத்தில் இருந்து 21 August 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210821050422/https://www.bbc.com/news/technology-35361090. 
  62. ↑ "GIMPS Project Discovers Largest Known Prime Number: 277,232,917-1". Great Internet Mersenne Prime Search. 3 January 2018 இம் மூலத்தில் இருந்து 4 January 2018 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20180104073001/https://www.mersenne.org/primes/?press=M77232917. 
  63. ↑ Lamb, Evelyn (4 January 2018). "Why You Should Care About a Prime Number That's 23,249,425 Digits Long". Slate Magazine (in ஆங்கிலம்). Archived from the original on 9 October 2021. பார்க்கப்பட்ட நாள் 13 October 2021.
  64. ↑ "GIMPS Discovers Largest Known Prime Number: 282,589,933-1". Great Internet Mersenne Prime Search. 21 December 2018 இம் மூலத்தில் இருந்து 22 December 2018 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20181222180200/https://www.mersenne.org/primes/?press=M82589933. 
  65. ↑ Palca, Joe (21 December 2018). "The World Has A New Largest-Known Prime Number" (in en). NPR இம் மூலத்தில் இருந்து 30 July 2021 அன்று. பரணிடப்பட்டது.. https://web.archive.org/web/20210730014914/https://www.npr.org/2018/12/21/679207604/the-world-has-a-new-largest-known-prime-number. 

வெளியிணைப்புகள்

தொகு
  • மெர்சென் பகாத்தனிக்களின் அடுக்கெண்களின் (p) தொடர்வரிசை:(OEIS-இல் வரிசை A000043)
  • செவ்விய எண்களின் தொடர்வரிசை:(OEIS-இல் வரிசை A000396)
  • மெர்சென் பகாத்தனிகளின் தொடர்வரிசை:(OEIS-இல் வரிசை A000668)
"https://ta.wikipedia.org/w/index.php?title=மெர்சென்_பகா_எண்கள்-செவ்விய_எண்கள்_பட்டியல்&oldid=3984702" இலிருந்து மீள்விக்கப்பட்டது