விகிதமுறா எண்

கணிதத்தில் இரண்டு முழு எண்களின் விகிதமாக, அல்லது பின்னங்களாக எழுதப்பட இயலாத அனைத்து மெய்யெண்களும் விகிதமுறா எண்கள் (irrational number) எனப்படும். இரு  கோட்டுத்துண்டுகளின்  நீளங்களின் விகிதம் ஒரு விகிதமுறா  எண் ஆகும் போது, கோட்டுத்துண்டுகளானது பொதுவான அளவினை கொண்டிருக்காது. அதாவது அவைகளுக்கு   நீளம் (அளவை) கிடையது, எவ்வளவு குறுகியதாய் இருந்தாலும், அந்த இரு கொடுக்கப்பட்ட கோட்டுத்துண்டுகளின் நீளங்கள் முழுக்களின் பெருக்கலாக இருக்கும்.

கணித மாறிலியான பை (π) என்பது ஒரு விகிதமுறா எண். இது அனைவருக்கும் தெரிந்த ஒன்று

மெய் எண்கள் (R) தொகுப்பில், விகிதமுறு (Q), முழுவெண் (Z), இயல் எண்கள் (N). இதில் அடங்கும். மேலும் விகிதமுறா (R\Q).எண்களும் மெய் எண்கள் தொகுப்பில் அடங்கும்.

$\scriptstyle {\sqrt {2}}$ ஒரு விகிதமுறா எண்ணாகும்.

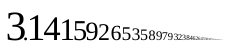
கணித வரலாற்றில் விகிதமுறா எண்களின் அறிமுகம் ஒரு முக்கியமான திருப்பமாகக் கருதப்படுகிறது. வட்டத்தின் சுற்றளவுக்கும் விட்டத்திற்கும் உள்ள விகிதம் π, e, φ, 2-இன் இருபடி மூலம் ஆகியவை முக்கிய நன்கு அறியப்பட்ட விகிதமுறா எண்கள் ஆகும். உண்மையில், செவ்விய இருபடிகள் தவிர்த்து, இயல் எண்களின் இருபடி மூலங்கள் விகிதமுறா எண்களாகும்.

எண் முறையினத்தை விரிவுபடுத்தப்படும் போது (எ.கா. தசம எண்கள் அல்லது வேறு எந்த இயல் அடிப்படையிலானது), விகிதமுறா எண்கள் முடிவற்றது, அல்லது மீளும் தசமங்கள் அல்ல எனக் காட்டப்படலாம். அதாவது, இலக்கங்களின் மீண்டும் மீண்டும் வரும் எண்தொடர்ச்சியை கொண்டிருக்காது, எ.கா. எண் π இன் தசம வடிவமானது  3.14159265358979 உடன் தொடங்குகிறது. ஆனால் முடிவற்ற எண் வரிசையில்  மீண்டும் மீண்டும் வரும் எண்தொடர்ச்சியை π கொண்டிருக்காது. ஒரு விகிதமுறு எண்ணின் தசம விரிவாக்கம் முடிவடைதல் வேண்டும் அல்லது திரும்பத் திரும்ப வேண்டும் என்பது நிரூபணமானதாக இருக்க வேண்டும் என்பதற்கான ஆதாரம், ஒரு தசம விரிவாக்கம் முடிவடைகிறது அல்லது மீண்டும் நிகழும் ஒரு பகுதியாக இருக்க வேண்டும், மேலும் அடிப்படை மற்றும் நீளமானதாக இருந்தாலும், இரண்டு சான்றுகள் விகிதமுறு எண்ணின் கருத்தக அமைகின்றன.

விகிதமுறா எண்கள் கூட முடிக்கப்படாத தொடர்ச்சியான பின்னங்கள் மூலம் தீர்க்கப்பட வேண்டும்.

மெய் எண்கள் கணக்கிட முடியாத மற்றும் விகிதமுறு கணக்கிடக்கூடிய எண்கள் என்னும் கேண்டரின் நிறுவலின் விளைவாக, கிட்டத்தட்ட அனைத்து மெய்யான எண்களும் விகிதமுறா எண்கள்களாக உள்ளன.

வரலாறு

வர்க்கமூலங்கள் போன்ற விகிதமுறு எண்களின் இருப்பு பண்டைய இந்தியாவில் வேதகாலம் முதற்கொண்டே அறியப்பட்டிருந்தது. விகிதமுறா எண் எனும் எண்ணக்கரு, மானவர் (கி.மு 750 - கி.மு 690) என்னும் இந்திய கணிதவியலாளரினால் 2, 61 போன்ற எண்களுக்கான வர்க்கமூலங்கள் திருத்தமாக துல்லியமான பெறுமானங்களுக்கு கணிக்க முடியாது என்ற கருத்தை முன்வைக்கும் போதே 7ம் நூற்றாண்டளவில் ஏனைய இந்திய கணிதவியலாளர்களால் ஏற்றுக்கொள்ளப்பட்டதாகக் கருதப்படுகிறது.

எடுத்துக்காட்டுகள்

வர்க்கமூலங்கள்

2 இன் வர்க்கமூலமே, முதன்முதலாக விகிதமுறா எண் என்று நிறுவப்பட்ட எண் ஆகும். 2 இன் வர்க்கமூலம் ஒரு விகிதமுறா எண் என்பதற்கான நிறுவல்கள் பல உள்ளன. நன்கறியப்பட்ட மற்றொரு விகிதமுறா எண் பொன் விகிதம் ஆகும். முழு வர்க்கமாக இல்லாத அனைத்து இயல் எண்களின் வர்க்கமூலங்களும் விகிதமுறா எண்களாகும்.

பொது மூலங்கள்

2 இன் வர்க்கமூலம் ஒரு விகிதமுறா எண் என்பதன் நிறுவலை எண்கணிதத்தின் அடிப்படைத் தேற்றத்தைக் கொண்டு பொதுமைப்படுத்தலாம். இதன்மூலம் ஒவ்வொரு முழுவெண்ணுக்கும் தனித்ததொரு பகாக் காரணிப்படுத்தும் முறை உள்ளது என்பதையும் உறுதி செய்யமுடியும். அதனைக்கொண்டு, சுருக்கவியலாப் பின்னத்தில் அதன் பகுதி மற்றும் தொகுதியை எந்த அடுக்குக்கு உயர்த்தினாலும் தொகுதியை வகுக்க முடியாத ஒரு பகாஎண் அதன் பகுதியில் உண்டு என்ற கூற்றுக்கிணங்க, ஒரு விகிதமுறு எண்ணானது ஒரு முழுவெண் இல்லையெனில், அதன் எந்தவொரு முழுவெண் அடுக்கும் முழுவெண்ணாக இருக்காது என்பதையும் காட்டமுடியும். எனவே ஒரு முழுவெண்ணானது எந்தவொரு முழுவெண்ணின் k^ஆவது அடுக்காக அமையாது எனில், அதன் k^ஆவது மூலம் ஒரு விகிதமுறா எண்ணாகும்.

மடக்கைகள்

சில மடக்கைகள், விகிதமுறா எண்களென எளிதில் நிறுவக்கூடியவையாகும்.

எடுத்துக்காட்டுகள்:

• log₂ 3 ஒரு விகிதமுறா எண்
• log₁₀ 2 ஒரு விகிதமுறா எண்

நிறுவல்: log₂ 3 ஒரு விகிதமுறா எண் என்பதற்கான எதிர்மறுப்பு நிறுவல்: :log₂ 3 ≈ 1.58 > 0.

log₂ 3 விகிதறு எண் எனக்கொள்க.

எனவே, $\log _{2}3={\frac {m}{n}}.$, இதில் m , n என்பன நேர்ம முழுவெண்கள்.

இதிலிருந்து,

$2^{m/n}=3$

$(2^{m/n})^{n}=3^{n}$

$2^{m}=3^{n}.$

ஆனால் 2 இன் எந்தவொரு அடுக்கும் இரட்டை எண்ணாகும்; அதேபோல 3 இன் எந்தவொரு அடுக்கும் ஒற்றையெண்ணாகும். மேலும் எந்தவொரு முழுவெண்ணும் ஒரேசமயத்தில் இரட்டையெண்ணாகவும் ஒற்றையெண்ணாகவும் இருக்கமுடியாது. எனவே மேலுள்ள இறுதிக் கூற்று ஒரு முரண்பாடாகும். எனவே நாம் எடுத்துக்கொண்ட "log₂ 3 ஒரு விகிதமுறு எண்" என்ற அனுமானம் தவறாகும். அதாவது, log₂ 3 ஒரு விகிதமுறா எண்; அதனை ஒருபோதும் முழுவெண்களின் பின்னவடிவில் (m/n with n ≠ 0) எழுதவியலாது.

இதேமுறையில் log₁₀ 2 க்கும் நிறுவலாம்.

தசம வடிவங்கள்

ஒரு விகிதமுறு எண்ணின் தசம பின்ன வடிவானது ஒருபோதும் முடிவுறு தசம பின்னமாகவோ அல்லது மீள்தசமமாகவோ இருக்காது. பத்தடிமான எண்களுக்கு மட்டுமல்லாது, இவ்வுண்மை ஈரடிமான முறைமை, எண்ணெண் முறைமை அல்லது பதினறும எண் முறைமைகளுக்கும் பொருந்தும். அதாவது பொதுவாக, இயல் எண் அடிமான இடஞ்சார் குறியீட்டு எண்குறி முறைமைகள் எல்லாவற்றுக்கும் இது பொருந்தும்.

முடிவுறும் தசமங்களும் மீளும் தசமங்களும் விகிதமுறு எண்கள்; அவற்றை பின்ன வடிவிற்கு மாற்றலாம் என்பதை எளிதாக நிறுவலாம்.

எடுத்துக்காட்டு:

மீளும் தசமம்:

$A=0.7\,162\,162\,162\,\cdots .$

இருபுறமும் 10 ஆல் பெருக்க:

$10A=7.162\,162\,162\,\cdots .$

மீண்டும் இருபுறமும் 10³ (where 3 என்பது மீளும் தசமங்களின் எண்ணிக்கை

$10,000A=7\,162.162\,162\,\cdots .$

10,000A சமன்பாட்டிலிருந்து 10A சமன்பாட்டைக் கழிக்க:

$9990A=7155.$

$A={\frac {7155}{9990}}$ (விகிதமுறு எண்)

விடை தெரியாத வினாக்கள்

• π + e (அல்லது π − e) விகிதமுறா எண்ணா இல்லையா என்பது அறியப்படவில்லை.
• mπ + ne என்பது விகிதமுறா எண்ணாக இருக்குமாறு m , n இரண்டிற்குமான எந்தவொரு பூச்சியமற்ற முழுவெண் மதிப்புகளும்.
• πe, π/e, 2^e, π^e, π^√2, இயல் மடக்கை π,கேட்டலான் மாறிலி ஆகியவை விகிதமுறா எண்களா இல்லையா என்பதும் கண்டறியப்படவில்லை.
• ⁿπ, ⁿe முழுவெண் n > 1 விகிதமுறு எண்களா என்பதும் அறியப்படவில்லை.

இவற்றையும் பார்க்கவும்

• விகிதமுறாமூலம்
• விகிதமுறு எண்